Les dérivées des fonctions trigonométriques
Pour toutes ces fonctions trigonométriques, on aura pour chacune leur fonction réciproque.
Entre une fonction et sa fonction réciproque, on a la relation :
$$ f \circ f^{-1} = id$$
Un exemple avec la fonction \(sin(x)\) et \(arcsin(x)\) :
$$ \Biggl \{ \begin{gather*}
f : x \longmapsto sin(x), \hspace{3.1em} \mathbb{R } \longmapsto [-1, \enspace 1] \\
f^{-1} : x \longmapsto arcsin(x), \enspace [-1, \enspace 1] \longmapsto \mathbb{R } \end{gather*} $$
$$ arcsin(sin(x)) = x \Longleftrightarrow sin(arcsin(x)) = x $$
Attention à ne pas confondre la notation "\( f^{-1} \)" des fonctions réciproques avec celle de l'inverse.
En effet, on note "\( cos^{-1}, \ sin^{-1}, \ tan^{-1}... \)" pour les fonctions réciproques des fonctions trigonométriques \( (arcsin, \ arccos, \ arctan...) \), mais c'est une notation différente de "\( f^{-1} \)" qui signifie en général la fonction inverse \( (x^{-1} = \frac{1}{x}) \).
$$ cos^2(x) = cos(x)cos(x) $$
$$ (mais) $$
$$ \Biggl[ cos^{-1}(x) = arccos(x) \Biggr] \ \neq \ \Biggl[ \Bigl(cos(x)\Bigr)^{-1} = \frac{1}{cos(x)} = sec(x) \Biggr] $$
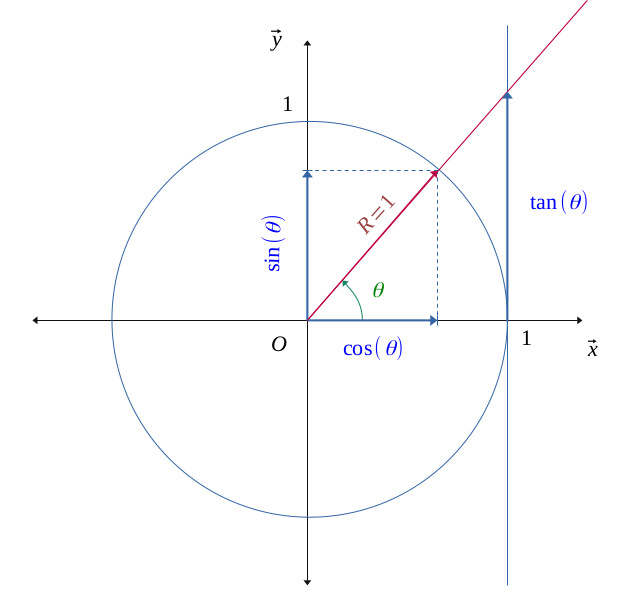
En appliquant le théorème de Thalès, on voit bien la relation :
$$ \frac{cos(\theta)}{1} = \frac{sin(\theta)}{tan(\theta)} \Longleftrightarrow tan(\theta) = \frac{sin(\theta)}{cos(\theta)} $$
La fonction \( sin(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sin(x) $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ sin(x)' = cos(x) $$
La fonction \( cos(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = cos(x) $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ cos(x)' = -sin(x) $$
La fonction \( tan(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = tan(x) = \frac{sin(x)}{cos(x)} $$
Elle admet pour dérivée :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr] $$
$$ tan(x)' = 1 + tan^2(x) = \frac{1}{cos^2(x)}= sec^2(x) $$
La fonction \( arcsin(x) \) est la fonction réciproque de la fonction \( sin(x) \), elle est définie de la manière suivante :
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arcsin(x) = sin^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-1 ,\hspace{0.2em} 1[, $$
$$ arcsin(x)' = \frac{1}{\sqrt{1 - x^2}} $$
La fonction \( arccos(x) \) est la fonction réciproque de la fonction \( cos(x) \), elle est définie de la manière suivante :
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arccos(x) = cos^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-1 , \hspace{0.2em}1[, $$
$$ arccos(x)' = -\frac{1}{\sqrt{1 - x^2}} $$
La fonction \( arctan(x) \) est la fonction réciproque de la fonction \( tan(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = arctan(x) = tan^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ arctan(x)' = \frac{1}{1 + x^2} $$
Les trois fonctions trigonométriques sécantes sont les fonctions \( cosec(x), sec(x) \) et \( cotan(x) \).
Elles sont respectivement les inverses des fonctions \( sin(x), cos(x) \) et \( tan(x) \).
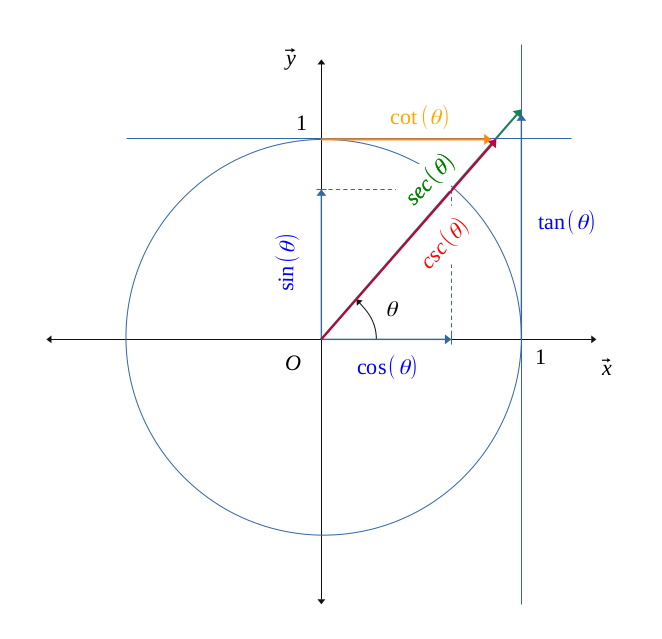
En appliquant le théorème de Thalès, on voit bien les relations :
$$ \left \{ \begin{gather*}
\frac{cosec(\theta)}{1} = \frac{1}{sin(\theta)} \Longleftrightarrow cosec(\theta) = \frac{1}{sin(\theta)} \\
\frac{sec(\theta)}{1} = \frac{1}{cos(\theta)} \Longleftrightarrow sec(\theta) = \frac{1}{cos(\theta)} \\
\frac{cotan(\theta)}{1} = \frac{cosec(\theta)}{sec(\theta)} = \frac{1}{tan(\theta)} \Longleftrightarrow cotan(\theta) = \frac{1}{tan(\theta)}
\end{gather*} \right \} $$
La fonction \( cosec(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], \enspace f(x) = cosec(x) = \frac{1}{sin(x)} $$
Elle admet pour dérivée :
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cosec(x)' = - cosec^2(x)cos(x) = -cosec(x)cotan(x) $$
On remarque par ailleurs que :
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ \frac{cosec'(x)}{cosec(x)} = -cosec(x)cos(x) = -tan(x)$$
La fonction \( sec(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = sec(x) = \frac{1}{cos(x)} $$
Elle admet pour dérivée :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ sec(x)' = sec^2(x) sin(x) = sec(x)tan(x) $$
On remarque par ailleurs que :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ \frac{sec'(x)}{sec(x)} = sec(x)sin(x) = tan(x)$$
La fonction \( cotan(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr] , \enspace f(x) = cotan(x) = \frac{cosec(x)}{sec(x)} = \frac{1}{tan(x)} $$
Elle admet pour dérivée :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cotan(x)' = -(1 + cotan^2(x)) = - cosec^2(x) $$
La fonction \( arccosec(x) \) est la fonction réciproque de la fonction \( cosec(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccosec(x) = cosec^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
La fonction \( arcsec(x) \) est la fonction réciproque de la fonction \( sec(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arcsec(x) = sec^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arcsec(x)' = \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
La fonction \( arccotan(x) \) est la fonction réciproque de la fonction \( cotan(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R} , \enspace f(x) = arccotan(x) = cotan^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ arccotan(x)' = - \frac{1}{ 1 + x^2} $$
Les trois fonctions hyperboliques sont fonctions \( sinh(x), cosh(x) \) et \( tanh(x) \).
Elles sont le pendant respectif des fonctions \( sin(x), cos(x) \) et \( tan(x) \), notamment au niveau des propriétés.
La fonction \( sinh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sinh(x) = \frac{e^x - e^{-x} }{2} $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ sinh(x)' = cosh(x) $$
La fonction \( cosh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = cosh(x) = \frac{e^x + e^{-x} }{2} $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ cosh(x)' = sinh(x) $$
La fonction \( tanh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = tanh(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ tanh(x)' = 1 - tanh^2(x) = sech^2(x) $$
La fonction \( arcsinh(x) \) est la fonction réciproque de la fonction \( sinh(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = arcsinh(x)= sinh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$ \forall x \in \mathbb{R},$$
$$ arcsinh(x) = ln \left|x + \sqrt{x^2 + 1}\right| $$
(\(\Longrightarrow\) voir la démonstration)
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + x^2}} $$
La fonction \( arccosh(x) \) est la fonction réciproque de la fonction \( cosh(x) \), elle est définie de la manière suivante :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, \enspace f(x) = arccosh(x) = cosh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x) = ln \Bigl| x + \sqrt{x^2 - 1}\Bigr| $$
(\(\Longrightarrow\) voir la démonstration)
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x)' = \frac{1}{\sqrt{x^2 -1}} $$
La fonction \( arctanh(x) \) est la fonction réciproque de la fonction \( tanh(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, \enspace f(x) = arctanh(x) = tanh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$\forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[,$$
$$ arctanh(x) = \frac{1}{2} ln \left| \frac{1 + x}{1 - x} \right| $$
(\(\Longrightarrow\) voir la démonstration)
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x)' = \frac{1}{1 - x^2} $$
Les trois fonctions sécantes hyperboliques sont les fonctions \( cosech(x), sech(x) \) et \(cotanh(x) \).
Elles sont respectivement les inverses des fonctions \( sinh(x), cosh(x) \) et \( tanh(x) \).
La fonction \( cosech(x) \) est définie de la manière suivante :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cosech(x) = \frac{1}{sinh(x)} $$
Elle admet pour dérivée :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cosech(x)' = - cosech^2(x) cosh(x) = -cosech(x)cotanh(x) $$
On remarque par ailleurs que :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ \frac{cosech'(x)}{cosech(x)} = -cosech(x)cosh(x) = -cotanh(x)$$
La fonction \( sech(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sech(x) = \frac{1}{cosh(x)} $$
Elle admet pour dérivée :
$$ \forall x \in \mathbb{R}, $$
$$ sech(x)' = -sech^2(x)sinh(x) = -sech(x)tanh(x) $$
On remarque par ailleurs que :
$$ \forall x \in \mathbb{R}, $$
$$ \frac{sech'(x)}{sech(x)} = -sech(x)sinh(x) = -tanh(x)$$
La fonction \( cotanh(x) \) est définie de la manière suivante :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cotanh(x) = \frac{1}{tanh(x)} $$
Elle admet pour dérivée :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cotanh(x)' = 1 - cotan^2(x) = -cosech^2(x)$$
La fonction \( arccosech(x) \) est la fonction réciproque de la fonction \( cosech(x) \), elle est définie de la manière suivante :
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , \enspace f(x) = arccosech(x) = cosech^{-1}(x) $$
Elle admet pour dérivée :
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , $$
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 + \frac{1}{ x^2}}} $$
La fonction \( arcsech(x) \) est la fonction réciproque de la fonction \( sech(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]0, \hspace{0.1em} 1] , \enspace f(x) = arcsech(x) = sech^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.1em} ]0, \hspace{0.1em} 1], $$
$$ arcsech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{\frac{1}{ x^2} - 1}} $$
La fonction \( arccotanh(x) \) est la fonction réciproque de la fonction \( cotanh(x) \), elle est définie de la manière suivante :
$$ \forall \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccotanh(x) =cotanh^{-1}(x) $$
Elle admet pour dérivée :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccotanh(x)' = \frac{1}{ 1 - x^2} $$
Démonstrations
La fonction \( sin(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sin(x) $$
Avec la définition de la dérivée, on a :
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x + h) - sin(x)}{h} $$
Avec les formules d'addition trigonométriques, on sait que :
$$ \forall (\alpha, \beta) \in \hspace{0.04em} \mathbb{R}^2, $$
$$ sin(\alpha + \beta) = sin(\alpha) cos(\beta) + cos(\alpha) sin(\beta) $$
Soit :
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x) cos(h) + cos(x) sin(h) - sin(x)}{h} $$
Lorsque \( h \to 0\), \( cos(h) \to 1\) et \( sin(h) \to h\).
Et,
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x) + cos(x). h - sin(x)}{h} $$
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{cos(x). h }{h} $$
Soit finalement,
$$ \forall x \in \mathbb{R}, $$
$$ sin(x)' = cos(x) $$
La fonction \( cos(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = cos(x) $$
Avec la définition de la dérivée, on a :
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x + h) - cos(x)}{h} $$
Avec les formules d'addition trigonométriques, on sait que :
$$ \forall (\alpha, \beta) \in \hspace{0.04em} \mathbb{R}^2, $$
$$ cos(\alpha + \beta) = cos(\alpha) cos(\beta) - sin(\alpha) sin(\beta) $$
Soit :
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x) cos(h) - sin(x) sin(h) - cos(x)}{h} $$
Lorsque \( h \to 0\), \( cos(h) \to 1\) et \( sin(h) \to h\).
Et,
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x) - sin(x). h - cos(x)}{h} $$
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ - sin(x). h }{h} $$
Soit finalement,
$$ \forall x \in \mathbb{R}, $$
$$ cos(x)' = -sin(x) $$
La fonction \( tan(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = tan(x) = \frac{sin(x)}{cos(x)} $$
Par définition,
$$ tan(x)' = \left( \frac{sin(x)}{cos(x)} \right)' $$
Avec la dérivée d'un quotient, on sait que :
$$ \forall (f,g), \ g \neq 0, $$
$$ \left ( f \over g \right)' = \frac{f'g - g'f}{g^2} $$
Soit dans notre cas :
$$ tan(x)' = \frac{cos(x)cos(x) + sin(x)sin(x)}{cos^2(x)} $$
$$ tan(x)' = \frac{cos^2(x) + sin^2(x)}{cos^2(x)} $$
$$ tan(x)' = \frac{cos^2(x) + sin^2(x)}{cos^2(x)} $$
Et finalement,
$$ \forall k \in \mathbb{Z}, \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr] $$
$$ tan(x)' = 1 + tan^2(x) = \frac{1}{cos^2(x)} = sec^2(x) $$
La fonction \( arcsin(x) \) est la fonction réciproque de la fonction \( sin(x) \), elle est définie de la manière suivante :
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arcsin(x) = sin^{-1}(x) $$
On peut calculer cette dérivée en passant par la dérivée d'une fonction réciproque :
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = sin(x) \\
f'(x) = cos(x) \\
f^{-1}(x) = arcsin(x) \end{gather*} \right \} $$
Par suite,
$$ arcsin(x)' = \frac{1}{cos(arcsin(x))} $$
Par ailleurs,
$$ cos^2(x) + sin^2(x) = 1$$
$$ cos^2(x) = 1 - sin^2(x) $$
$$ | cos(x) | = \sqrt{1 - sin^2(x)} $$
Or, la fonction \(arcsin(x)\) étant définie quand \( x \in \bigl[-1; 1\bigr]\) à valeurs dans \(\left[-\frac{\pi}{2}; \frac{\pi}{2} \right]\), la fonction \(cos(arcsin(x))\) est toujours positive car la fonction \(cos(X)\) est positive quand \(X \in \left[-\frac{\pi}{2}; \frac{\pi}{2} \right]\).
$$x \longmapsto arcsin(x)$$
$$\bigl[-1; 1\bigr] \longmapsto \left[-\frac{\pi}{2}; \frac{\pi}{2} \right]$$
$$ \hspace{12em} X \longmapsto cos(X)$$
$$\hspace{12em} \left[-\frac{\pi}{2}; \frac{\pi}{2} \right] \longmapsto \bigl[0; 1\bigr]$$
Soit dans notre cas, on peut garder uniquement le cas positif :
$$ cos(arcsin(x)) = \sqrt{1 - sin^2(arcsin(x))} $$
Donc en remplaçant on a,
$$ arcsin(x)' = \frac{1}{\sqrt{1 - sin^2(arcsin(x))}} $$
Soit finalement,
$$ \forall x \in \hspace{0.04em} ]-1 ,\hspace{0.2em} 1[, $$
$$ arcsin(x)' = \frac{1}{\sqrt{1 - x^2}} $$
La fonction \( arccos(x) \) est la fonction réciproque de la fonction \( cos(x) \), elle est définie de la manière suivante :
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arccos(x) = cos^{-1}(x) $$
Exactement par le même procédé que pour le calcul de \(arcsin(x)'\) ci-dessus :
$$ arccos(x)' = - \frac{1}{\sqrt{1 - cos^2(arccos(x))}} $$
Soit finalement,
$$ \forall x \in \hspace{0.04em} ]-1 , \hspace{0.2em}1[, $$
$$ arccos(x)' = -\frac{1}{\sqrt{1 - x^2}} $$
La fonction \( arctan(x) \) est la fonction réciproque de la fonction \( tan(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = arctan(x) = tan^{-1}(x) $$
Exactement par le même procédé que pour le calcul de \(arcsin(x)'\) ci-dessus :
$$ arctan(x)' = \frac{1}{1 + tan^2(arctan(x))} $$
Soit finalement,
$$ \forall x \in \mathbb{R}, $$
$$ arctan(x)' = \frac{1}{1 + x^2} $$
La fonction \( cosec(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], \enspace f(x) = cosec(x) = \frac{1}{sin(x)} $$
Par définition, on a :
$$ cosec(x)' = \biggl(\frac{1}{sin(x)} \biggr)' $$
Soit ici,
$$ cosec(x)' = -\frac{cos(x)}{sin^2(x)} $$
Et finalement,
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cosec(x)' = - cosec^2(x)cos(x) = -cosec(x)cotan(x) $$
On remarque par ailleurs que :
$$ \frac{cosec'(x)}{cosec(x)} = \frac{-cosec^2(x)cos(x)}{cosec(x)} $$
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ \frac{cosec'(x)}{cosec(x)} = -cosec(x)cos(x) = -tan(x)$$
La fonction \( sec(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = sec(x) = \frac{1}{cos(x)} $$
Par définition :
$$ sec(x)' = \biggl(\frac{1}{cos(x)} \biggr)' $$
On applique encore la dérivée de l'inverse d'une fonction :
$$ sec(x)' = \frac{sin(x)}{cos^2(x)} $$
Et finalement,
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ sec(x)' = sec^2(x) sin(x) = sec(x)tan(x) $$
On remarque par ailleurs que :
$$ \frac{sec'(x)}{sec(x)} = \frac{sec^2(x)tan(x)}{sec(x)} $$
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ \frac{sec'(x)}{sec(x)} = sec(x)sin(x) = tan(x)$$
La fonction \( cotan(x) \) est définie de la manière suivante :
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr] , \enspace f(x) = cotan(x) = \frac{cosec(x)}{sec(x)} = \frac{1}{tan(x)} $$
Par définition :
$$ cotan(x)' = \biggl(\frac{1}{tan(x)} \biggr)' $$
On applique encore la dérivée de l'inverse d'une fonction.
$$ cotan(x)' = - \frac{1 + tan^2(x)}{tan^2(x)} $$
Et finalement,
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cotan(x)' = -(1 + cotan^2(x)) = - cosec^2(x) $$
La fonction \( arccosec(x) \) est la fonction réciproque de la fonction \( cosec(x) \), elle est définie de la manière suivante :
On peut calculer cette dérivée en passant par la dérivée d'une fonction réciproque :
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = cosec(x) \\
f'(x) = - cosec^2(x)cos(x) \\
f^{-1}(x) = arccosec(x) \end{gather*} \right \} $$
$$ arccosec(x)' = -\frac{1}{cosec^2(arccosec(x)) \times cos(arccosec(x))} $$
Par ailleurs,
$$ cos^2(x) + sin^2(x) = 1$$
$$ cos^2(x) = 1 - sin^2(x) $$
$$ | cos(x) | = \sqrt{1 - sin^2(x)} $$
Or, la fonction \(arccosec(x)\) étant définie quand \( x \in \bigl[-\infty; -1\bigr] \cup \bigl[1; +\infty\bigr] \) à valeurs dans \(\left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \), la fonction \(cos(arcsin(x))\) est toujours positive car la fonction \(cos(X)\) est positive quand \( X \in \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \).
$$\hspace{6em} x \longmapsto arccosec(x)$$
$$\bigl[-\infty; -1\bigr] \cup \bigl[1; +\infty\bigr] \longmapsto \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right]$$
$$ \hspace{16em} X \longmapsto cos(X)$$
$$\hspace{16em} \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \longmapsto \bigl[0; 1\bigr]$$
Soit dans notre cas, on peut garder uniquement le cas positif :
$$ cos(arccosec(x)) = \sqrt{1 - sin^2(arccosec(x))} $$
$$ arccosec(x)' = -\frac{1}{cosec^2(arccosec(x)) \times \sqrt{1 - sin^2(arccosec(x))}} $$
Mais :
$$ cosec(x) = \frac{1}{sin(x)} \Longleftrightarrow sin(x) = \frac{1}{cosec(x)} $$
Soit,
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{cosec^2(arccosec(x))}}} $$
Soit finalement,
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
La fonction \( arcsec(x) \) est la fonction réciproque de la fonction \( sec(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arcsec(x) = sec^{-1}(x) $$
Exactement par le même procédé que pour le calcul \(arccosec(x)'\) ci-dessus :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arcsec(x)' = \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
La fonction \( arccotan(x) \) est la fonction réciproque de la fonction \( cotan(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R} , \enspace f(x) = arccotan(x) = cotan^{-1}(x) $$
Exactement par le même procédé que pour le calcul de \(arccosec(x)'\) ci-dessus :
$$ \forall x \in \mathbb{R}, $$
$$ arccotan(x)' = - \frac{1}{ 1 + x^2} $$
La fonction \( sinh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sinh(x) = \frac{e^x - e^{-x} }{2} $$
Ici, on va juste faire varier les exponentielles en utilisant la dérivation en chaîne :
$$ sinh(x)' = \biggl(\frac{e^x - e^{-x}}{2} \biggr)' $$
$$ sinh(x)' = \frac{1}{2} \bigl( e^x + e^{-x} \bigr) $$
$$ sinh(x)' = \biggl(\frac{e^x + e^{-x}}{2} \biggr) $$
Et finalement,
$$ \forall x \in \mathbb{R}, $$
$$ sinh(x)' = cosh(x) $$
La fonction \( cosh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = cosh(x) = \frac{e^x + e^{-x} }{2} $$
On utilise exactement le même procédé que pour le calcul de \(sinh(x)'\) :
$$ cosh(x)' = \biggl(\frac{e^x + e^{-x}}{2} \biggr)' $$
$$ cosh(x)' = \frac{1}{2} \bigl( e^x - e^{-x} \bigr) $$
$$ cosh(x)' = \biggl(\frac{e^x - e^{-x}}{2} \biggr) $$
Et finalement,
$$ \forall x \in \mathbb{R}, $$
$$ cosh(x)' = sinh(x) $$
La fonction \( tanh(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = tanh(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
Par définition, on a :
$$ tanh(x)' = \biggl(\frac{e^x - e^{-x}}{e^x + e^{-x}} \biggr)' $$
On applique la dérivée d'un quotient :
$$ tanh(x)' = \frac{(e^x + e^{-x}) (e^x + e^{-x}) - (e^x - e^{-x})(e^x - e^{-x})}{(e^x + e^{-x})^2} $$
$$ tanh(x)' = \frac{(e^x + e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2} $$
$$ tanh(x)' = 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2} $$
Et finalement,
$$ \forall x \in \mathbb{R}, $$
$$ tanh(x)' = 1 - tanh^2(x) = sech^2(x) $$
La fonction \( arcsinh(x) \) est la fonction réciproque de la fonction \( sinh(x) \), elle est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = arcsinh(x)= sinh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$ \forall x \in \mathbb{R}, \ $$
$$ arcsinh(x) = ln \left|x + \sqrt{x^2 + 1}\right| $$
(\(\Longrightarrow\) voir la démonstration)
On peut calculer cette dérivée en passant par la dérivée d'une fonction réciproque :
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = sinh(x) \\
f('x) = cosh(x) \\
f^{-1}(x) = arcsinh(x) \end{gather*} \right \} $$
$$ arcsinh(x)' = \frac{1}{cosh(arcsinh(x))} $$
Par ailleurs,
$$ cosh^2(x) -sinh^2(x) = 1$$
$$ cosh^2(x) = 1 + sinh^2(x) $$
$$ | cosh(x) | = \sqrt{1 +sinh^2(x)} $$
Comme la fonction \(cosh(x)\) est toujours positive quand \(x \in \mathbb{R}\), on dire conserver le cas positif :
$$ cosh(x) = \sqrt{1 + sinh^2(x)} $$
Soit, en remplaçant on a :
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + sinh^2(arcsinh(x))}} $$
Soit finalement,
$$ \forall x \in \mathbb{R}, $$
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + x^2}} $$
La fonction \( arccosh(x) \) est la fonction réciproque de la fonction \( cosh(x) \), elle est définie de la manière suivante :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, \enspace f(x) = arccosh(x) = cosh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, $$
$$arccosh(x) = ln \Bigl| x + \sqrt{x^2 - 1}\Bigr| $$
(\(\Longrightarrow\) voir la démonstration)
Exactement par le même procédé que pour le calcul de \(arcsinh(x)'\) ci-dessus :
$$ \forall x \in \hspace{0.04em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x)' = \frac{1}{\sqrt{x^2 -1}} $$
La fonction \( arctanh(x) \) est la fonction réciproque de la fonction \( tanh(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, \enspace f(x) = arctanh(x) = tanh^{-1}(x) $$
Par ailleurs, elle peut aussi être définie explicitement par :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x) = \frac{1}{2} ln \left| \frac{1 + x}{1 - x} \right| $$
(\(\Longrightarrow\) voir la démonstration)
Exactement par le même procédé que pour le calcul de \(arcsinh(x)'\) ci-dessus :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x)' = \frac{1}{1 - x^2} $$
La fonction \( cosech(x) \) est définie de la manière suivante :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cosech(x) = \frac{1}{sinh(x)} $$
Par définition, on a :
$$ cosech(x)' = \biggl(\frac{1}{sinh(x)} \biggr)' $$
Soit ici,
$$ cosech(x)' = -\frac{cosh(x)}{sinh^2(x)} $$
Et finalement,
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cosech(x)' = - cosech^2(x) cosh(x) = -cosech(x)cotanh(x) $$
On remarque par ailleurs que :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ \frac{cosech'(x)}{cosech(x)} = -cosech(x)cosh(x) = -cotanh(x)$$
La fonction \( sech(x) \) est définie de la manière suivante :
$$ \forall x \in \mathbb{R}, \enspace f(x) = sech(x) = \frac{1}{cosh(x)} $$
Par définition, on a :
$$ sech(x)' = \biggl(\frac{1}{cosh(x)} \biggr)' $$
On applique encore la dérivée de l'inverse d'une fonction.
$$ sech(x)' = -\frac{sinh(x)}{cosh^2(x)} $$
Et finalement,
$$ \forall x \in \mathbb{R}, $$
$$ sech(x)' = -sech^2(x)sinh(x) = -sech(x)tanh(x) $$
On remarque par ailleurs que :
$$ \forall x \in \mathbb{R}, $$
$$ \frac{sech'(x)}{sech(x)} = -sech(x)sinh(x) = -tanh(x)$$
La fonction \( cotanh(x) \) est définie de la manière suivante :
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cotanh(x) = \frac{1}{tanh(x)} $$
Par définition, on a :
$$ cotanh(x)' = \biggl(\frac{1}{tanh(x)} \biggr)' $$
On applique encore la dérivée de l'inverse d'une fonction.
$$ cotanh(x)' = - \frac{1 - tanh^2(x)}{tanh^2(x)} $$
Et finalement,
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cotanh(x)' = 1 - cotan^2(x) = -cosech^2(x) $$
La fonction \( arccosech(x) \) est la fonction réciproque de la fonction \( cosech(x) \), elle est définie de la manière suivante :
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , \enspace f(x) = arccosech(x) = cosech^{-1}(x) $$
On peut calculer cette dérivée en passant par la dérivée d'une fonction réciproque :
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = cosech(x) \\
f'(x) = - cosech^2(x) \ cosh(x) \\
f^{-1}(x) = arccosech(x) \end{gather*} \right \} $$
$$ arccosech(x)' = \frac{1}{-cosech^2(arccosech(x)) \times cosh(arccosech(x))} $$
Par ailleurs,
$$ cosh^2(x) -sinh^2(x) = 1$$
$$ cosh^2(x) = 1 + sinh^2(x) $$
$$ | cosh(x) | = \sqrt{1 +sinh^2(x)} $$
Comme la fonction \(cosh(x)\) est toujours positive quand \(x \in \mathbb{R}\), on dire conserver le cas positif :
$$ cosh(x) = \sqrt{1 + sinh^2(x)} $$
Soit,
$$ arccosech(x)' = -\frac{1}{cosech^2(arccosech(x)) \times \sqrt{1 +sinh^2(arccosech(x))}} $$
Mais :
$$ cosech(x) = \frac{1}{sinh(x)} \Longleftrightarrow sinh(x) = \frac{1}{cosech(x)} $$
Soit,
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1+ \frac{1}{cosech^2(arccosech(x))}}} $$
Soit finalement,
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , $$
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 + \frac{1}{ x^2}}} $$
La fonction \( arcsech(x) \) est la fonction réciproque de la fonction \( sech(x) \), elle est définie de la manière suivante :
$$ \forall x \in \hspace{0.04em} ]0, \hspace{0.1em} 1] , \enspace f(x) = arcsech(x) = sech^{-1}(x) $$
Exactement par le même procédé que pour le calcul de \(arccosech(x)'\) ci-dessus :
$$ \forall x \in \hspace{0.1em} ]0, \hspace{0.1em} 1], $$
$$ arcsech(x)' = - \frac{1}{ x^2} \frac{1}{ \sqrt{1 + \frac{1}{ x^2}}} $$
La fonction \( arccotanh(x) \) est la fonction réciproque de la fonction \( cotanh(x) \), elle est définie de la manière suivante :
$$ \forall \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccotanh(x) =cotanh^{-1}(x) $$
Exactement par le même procédé que pour le calcul de \(arccosech(x)'\) ci-dessus :
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccotanh(x)' = \frac{1}{ 1 - x^2} $$





 Retour en haut de page
Retour en haut de page