Les critères de convergence des séries

Séries à termes positifs

Dans cette partie, il sera traité uniquement le cas des séries à termes positifs, mais le même principe s'applique alors aussi aux séries à termes négatifs, car si l'on considère deux séries :

une série à termes positifs : $S_+$
une série à termes positifs : $S_-$

Les deux varient seulement d'un signe $(-)$ en facteur :

$$ S_+ = - S_+ $$

Critère fondamental de convergence

Soit une suite $(u_n)_{n \in \mathbb{N}}$.

$$ \sum u_n \text{ converge } \Longrightarrow \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

Alors, si une suite admet une limite non nulle, on en déduit directement qu'elle est divergente.

Comparaison avec une série de référence

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs dont on souhaite connaître la nature.

On peut comparer cette suite terme à terme avec autre une suite $(U_n)_{n \in \mathbb{N}}$ dont la nature est connue.

$$ \Bigl[ s_n \leqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = M \Bigr] \Longrightarrow s_n \text{ converge et } (s_n < M) $$

$$ \text{avec : } \left \{ s_n = \sum_{k = 0}^n u_n, \hspace{2em} S_n = \sum_{k = 0}^n U_n \right \} $$

De manière symétrique, on a le complément :

$$ \Bigl[ s_n \geqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = + \infty \Bigr] \Longrightarrow s_n \text{ diverge} $$

Règle de D'Alembert

Si dans une série à termes positifs $\sum u_n$, on a toujours, à partir d'un certain rang :

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverge} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{on ne peut pas conclure} $$

$$ \text{(Règle de D'Alembert)}$$

Règle de Cauchy

Si dans une série à termes positifs $\sum u_n$, on a toujours, à partir d'un certain rang :

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverge} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{on ne peut pas conclure} $$

$$ \text{(Règle de Cauchy)}$$

Règle des $n^{\alpha} u_n$

Soit deux séries à termes positifs $\Bigl(\sum u_n, \sum v_n \Bigr)$.

Si l'on peut trouver $\alpha \in \mathbb{R}^*_+$ tel que :

$$ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

Alors,

$$ \alpha > 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \alpha \leqslant 1 \Longrightarrow \sum u_n \text{ diverge} $$

$$ \text{(Règle des $n^{\alpha} u_n$)}$$

Comparaison série-intégrale

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs et $f(n)$ sa fonction continue par morceaux associée décroissante.

On peut encadrer une série par deux intégrales pour en obtenir une approximation, tel que :

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

$$ (\text{avec } u_n = f(n)) $$

Séries alternées

Critère spécial des séries alternées

Pour toute suite décroissante à termes positifs $(u_n)_{n \in \mathbb{N}}$ et sa série alternée $(A_n)$ :

$$ \left[ \lim_{n \to \infty} u_n = 0 \right] \Longrightarrow A_n \text{ converge et } (A_n < u_1) $$

$$ \left(\text{avec } A_n = \sum_{k \geqslant 1} \Bigl[ (-1)^{k + 1} \ u_k \Bigr]\right) $$

Démonstrations

Séries à termes positifs

Critère fondamental de convergence

Soit une suite $(u_n)_{n \in \mathbb{N}}$ et $(S_n)$ sa série partielle associée, tels que :

$$ S_n = \sum_{k = 0}^n u_n $$

La convergence d'une telle série implique qu'il existe un certain entier naturel $p$ tel que :

$$ \lim_{n \to + \infty} \bigl[ S_{n + p} - S_n \bigr] = 0 \qquad (1) $$

Ce qui revient à dire que, si on fait la différence $ (S_{n + p} - S_n) $ :

$$ S_{n + p} - S_n = u_{n + 1} + u_{n + 2} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} $$

$$ avec \enspace \left \{ \begin{gather*} S_n = u_0 + u_1 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n - 1} + u_n \\ \\ S_{n + p} = u_0 + u_1 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n - 1} + u_n \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} \end{gather*} \right \} $$

Alors, en réécrivant $(1)$ sous sa nouvelle forme :

$$ \lim_{n \to + \infty} \bigl[ u_{n + 1} + u_{n + 2} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} \bigr] = 0 \qquad (1') $$

Comme cette condition est vraie pour toute valeur de $p$, avec $(p = 1)$, on a :

$$ \lim_{n \to + \infty} \bigl[ u_{n + 1} \bigr] = 0 $$

Ce qui est la même chose que d'écrire :

$$ \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

On a donc comme condition nécessaire, pour evnisager qu'une série converge, que sa suite associée soit de limite nulle.

$$ \sum u_n \text{ converge } \Longrightarrow \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

Alors, si une suite admet une limite non nulle, on en déduit directement qu'elle est divergente.

Comparaison avec une série de référence

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs dont on souhaite connaître la nature.

On peut comparer cette suite terme à terme avec autre une suite $(U_n)_{n \in \mathbb{N}}$ dont la nature est connue.

Supposons alors que tous les termes de la suite $(u_n)$ soient inférieurs ou égaux à ceux de la suite $(U_n)$, tel que :

$$ u_0 + u_1 + u_2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_n \leqslant U_0 + U_1 + U_2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} U_n $$

Posons :

$$ s_n = \sum_{k = 0}^n u_n $$

$$ S_n = \sum_{k = 0}^n U_n $$

D'après ce qui précède, on a :

$$ s_n \leqslant S_n $$

Supposons maintenant que la limite de $(U_n)$ soit connue :

$$ \exists M \in \mathbb{R}, \ \lim_{n \to +\infty} S_n = M $$

Par conséquent, on a toujours :

$$ s_n \leqslant S_n < M $$

Donc la série $(s_n)$ est aussi strictement majorée par $M$.

Comme c'est une série issue d'une suite à termes positifs, elle est croissante. Étant croissante et majorée, elle converge nécessairement.

$$ \Bigl[ s_n \leqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = M \Bigr] \Longrightarrow s_n \text{ converge et } (s_n < M) $$

$$ \text{avec : } \left \{ s_n = \sum_{k = 0}^n u_n, \hspace{2em} S_n = \sum_{k = 0}^n U_n \right \} $$

De manière symétrique, on a le complément :

$$ \Bigl[ s_n \geqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = + \infty \Bigr] \Longrightarrow s_n \text{ diverge} $$

Règle de D'Alembert

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs.

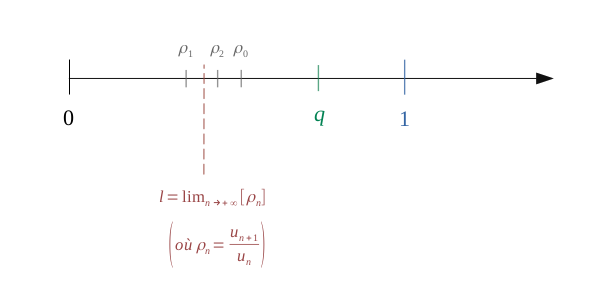
Admettons que le rapport $\left(\rho_n = \frac{u_{n + 1}}{u_n}\right)$ tende vers une certaine limite $l$ (finie ou une extrémité) :

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = l $$

si $(l < 1)$

Si $(l < 1)$, alors nous pouvons choisir un nombre naturel $(m \leqslant n)$ suffisamment grand, à partir duquel les prochains termes de la suite vont éventuellement osciller autour d'une certaine valeur, mais vont en tout cas converger vers cette dernière. On peut alors trouver un nouveau rapport $q$ qui lui sera toujours supérieur.

Dans ce cas,

$$ \frac{u_{m + 1}}{u_m} < q < 1 \qquad (H) $$

Cette hypothèse implique que :

$$ u_{m + 1} < u_m \ q $$

Alors, on peut établir une compraison entre un indice et le suivant :

$$ u_{m + 1} < u_m \ q $$

En multipliant par $q$ de chaque côté :

$$ u_{m + 1} \ q < u_m \ q^2 \qquad (2) $$

$$ u_{m + 2} < u_{m + 1} \ q \qquad (2') $$

Avec les deux expressions $(2)$ et $(2')$, on obtient :

$$ u_{m + 2} < u_{m + 1} \ q < u_m \ q^2 $$

Puis on peut répéter l'opération indéfiniment jusqu'à obtenir que :

$$ u_{m + p} < u_m \ q^p $$

Ainsi, chaque terme suivant $u_m$ est inférieur à celui d'une progression géométrique de raison $q$ :

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... < u_m + u_m \ q + u_m \ q^2 \hspace{0.2em} ... $$

Or, par notre hypothèse $(H)$, on a $(q < 1)$. Donc la série géométrique de raison $q$ converge, et il en est de même pour une série qui lui est inférieure terme à terme. Ainsi,

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converge} $$

si $(l > 1)$

En suivant le même raisonnement que pour le cas précédent, on s'aperçoit que :

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... > u_m + u_m \ q + u_m \ q^2 \hspace{0.2em} ... $$

Or ici $(q > 1)$, donc la série géométrique diverge, et il est de même pour la série $\sum u_n$ qui lui est supérieure terme à terme.

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverge} $$

si $(l = 1)$

Dans ce dernier cas, on ne peut rien affirmer de manière générale.

En effet, considérons la série suivante :

$$ \sum_{k = 1}^n \frac{1}{k^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \frac{1}{n^p} \qquad (\text{avec } p \in \mathbb{N}^*) $$

La rapport $\frac{u_{n + 1}}{u_n} $ à considérer est celui du terme général de sa suite associée : $u_n = \frac{1}{n^p} $, soit :

$$ \frac{u_{n + 1}}{u_ n} = \frac{\frac{1}{(n + 1)^p}}{\frac{1}{n^p}} $$

$$ \frac{u_{n + 1}}{u_ n} = \frac{n^p}{(n + 1)^p} $$

$$ \frac{u_{n + 1}}{u_ n} = \left(\frac{n}{n + 1} \right)^p $$

Qu'on peut arranger en :

$$ \frac{u_{n + 1}}{u_ n} = \left(\frac{n \textcolor{#606B9E}{+ 1 - 1}}{n + 1} \right)^p = \left(1 - \frac{1}{n + 1} \right)^p $$

Indépendamment de $p$, sa limite vaut :

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1^- $$

Or on sait que les séries de type $ \underset{k \leqslant 1}{\sum} \frac{1}{k^p}$ sont des séries de Riemann et:

si $(p = 1) $ : la série est divergente (série harmonique)
si $(p > 1) $ : la série est convergente

Ce contre-exemple montre bien qu'il n'existe pas de loi générale pour conclure sur la nature de la série, connaissant uniquement le résultat de la limite du rapport $\frac{u_{n + 1}}{u_n}$.

Alors,

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{on ne peut pas conclure} $$

Soit finalement,

Si dans une série à termes positifs $\sum u_n$, on a toujours, à partir d'un certain rang :

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverge} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{on ne peut pas conclure} $$

$$ \text{(Règle de D'Alembert)}$$

Règle de Cauchy

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs.

Cette règle ressemble beaucoup à la règle de D'Alembert, mais ici on étudiera le résultat de la limite de la racine $n$-ième du terme général de la suite $(u_n)$.

$$ \lim_{n \to \infty} \sqrt[n]{u_n} = l $$

si $(l < 1)$

Si $(l < 1)$, alors nous pouvons choisir un nombre naturel $(m \leqslant n)$ suffisamment grand, à partir duquel les prochains termes de la suite vont éventuellement osciller autour d'une certaine valeur, mais vont en tout cas converger vers cette dernière. On peut alors trouver une nouvelle racine $q$ qui lui sera toujours supérieure.

Dans ce cas,

$$ \sqrt[m]{u_m} < q < 1 \qquad (H^*) $$

Alors, on peut établir une compraison entre un indice et le suivant :

$$ \sqrt[m]{u_m} < q $$

$$ \sqrt[{m + 1}]{u_{m + 1}} < q $$

En prenant la puissance de chaque membre, on a :

$$ \left( \sqrt[m]{u_m} \right)^m < q^m $$

$$ u_m < q^m $$

$$ \left( \sqrt[m + 1]{u_{m + 1}} \right)^{m + 1} < q^{m + 1} $$

$$ u_{m + 1} < q^{m + 1} $$

Les termes de la série $\sum u_n$ sont donc tous inférieurs à celles d'une série géométrique de raison $q$ :

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... < q^n + q^{m + 1} + q^{m + 2} \hspace{0.2em} ... $$

Or, cette série converge car $(q < 1)$, donc il en est de même pour la série $\sum u_n$ qui lui est inférieure terme à terme.

Alors,

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converge} $$

si $(l > 1)$

En suivant le même raisonnement que pour le cas précédent, on s'aperçoit que :

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... > q^n + q^{m + 1} + q^{m + 2} \hspace{0.2em} ... $$

Or ici $(q > 1)$, donc la série géométrique diverge, et il est de même pour la série $\sum u_n$ qui lui est supérieure terme à terme.

$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverge} $$

si $(l = 1)$

Dans ce dernier cas, on ne peut rien affirmer de manière générale.

En effet, si on considère la même série que pour l'exemple précédent :

$$ \sum_{k = 1}^n \frac{1}{k^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \frac{1}{n^p} \qquad (\text{avec } q \in \mathbb{N}^*) $$

La racine à considérer $\sqrt[n]{u_n}$ est celui du terme général de sa suite associée : $u_n = \frac{1}{n^p} $, soit :

$$ \sqrt[n]{u_n} = \sqrt[n]{\frac{1}{n^p}} $$

$$ \sqrt[n]{u_n} = \left(\frac{1}{n^p}\right)^{\frac{1}{n}} $$

$$ \sqrt[n]{u_n} = \frac{1}{n^{\frac{p}{n}}} $$

Indépendamment de $p$, sa limite vaut :

$$ \lim_{n \to + \infty} \sqrt[n]{u_n} = 1 $$

Or on sait que les séries de type $ \underset{k \leqslant 1}{\sum} \frac{1}{k^p}$ sont des séries de Riemann et:

si $(p = 1) $ : la série est divergente (série harmonique)
si $(p > 1) $ : la série est convergente

Ce contre-exemple montre bien qu'il n'existe pas de loi générale pour conclure sur la nature de la série, connaissant uniquement le résultat de la racine $\sqrt[n]{u_n}$.

Alors,

$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{on ne peut pas conclure} $$

Soit finalement,

Si dans une série à termes positifs $\sum u_n$, on a toujours, à partir d'un certain rang :

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverge} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{on ne peut pas conclure} $$

$$ \text{(Règle de Cauchy)}$$

Règle des $n^{\alpha} u_n$

Soit $\alpha \in \mathbb{R}^*_+$ un réel strictement positif et $(v_n)_{n \in \mathbb{N}}$ une suite à termes positifs, tels que :

$$ \forall n \in \mathbb{N}^*, \ v_n = \frac{1}{n^{\alpha}} $$

Si on étudie le rapport $\frac{u_n}{v_n}$, on obtient :

$$ \frac{u_n}{v_n} = \frac{u_n}{\frac{1}{n^{\alpha}}} $$

$$ \frac{u_n}{v_n} = n^{\alpha} u_n $$

Or, on sait grâce à la propriété suivante que pour deux suites à termes de signe constant $(c_n, d_n)_{n \in \mathbb{N}}$ :

$$ \lim_{n \to + \infty} \left[ \frac{c_n}{d_n} \right] = l > 0 \Longrightarrow \text{$\sum c_n$ et $\sum d_n$ sont de même nature} $$

Mais on sait que les séries de type $\sum v_n$ sont des séries de Riemann et :

si $(\alpha > 1)$

Si $(\alpha > 1)$, alors la série $ \underset{k \leqslant 1}{\sum} \frac{1}{k^{\alpha}}$ est convergente.

Donc si l'on montre que :

$$ \exists \alpha > 1, \ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

On aura comme résultat que la série $\sum u_n$ converge aussi.

si $(\alpha \leqslant 1)$

Maintenant si $(\alpha \leqslant 1)$, alors la série $ \underset{k \leqslant 1}{\sum} \frac{1}{k^{\alpha}}$ est convergente, et si on arrive à montrer que:

$$ \exists \alpha \leqslant 1, \ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

On aura comme résultat que la série $\sum u_n$ diverge aussi.

Si l'on peut trouver $\alpha \in \mathbb{R}^*_+$ tel que :

$$ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

Alors,

$$ \alpha > 1 \Longrightarrow \sum u_n \text{ converge} $$
$$ \alpha \leqslant 1 \Longrightarrow \sum u_n \text{ diverge} $$

$$ \text{(Règle des $n^{\alpha} u_n$)}$$

Comparaison série-intégrale

Soit $(u_n)_{n \in \mathbb{N}}$ une suite à termes positifs et $f(n)$ sa fonction continue par morceaux associée décroissante.

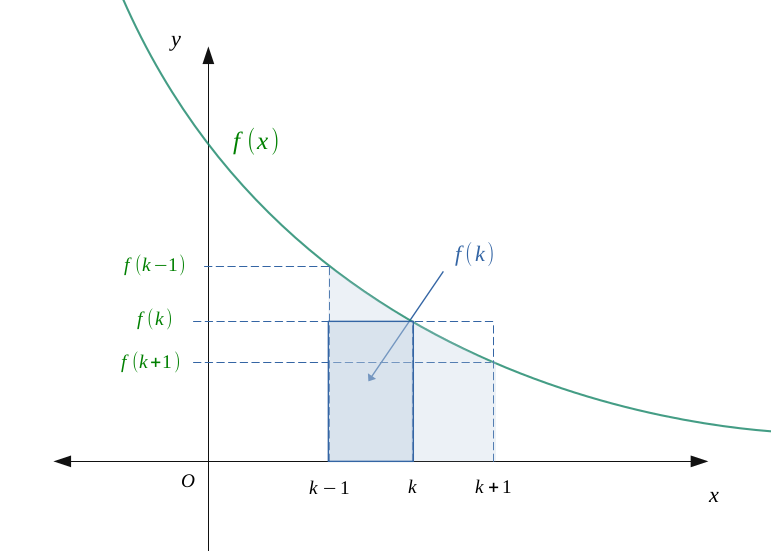
On a représenté un exemple sur la figure suivante :

Le rectangle mise en exergue vaut $f(k)$. On peut alors encadrer la série $\sum u_n$ par deux intégrales comme suit :

$$ \int_{k}^{k + 1} f(t) \ dt \leqslant f(k) \leqslant \int_{k - 1}^k f(t) \ dt $$

En sommant de $(k = 1)$ jusque $n$, on a :

$$ \sum_{k = 0}^n \left(\int_{k}^{k + 1} f(t) \ dt \right)\leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \left(\int_{k - 1}^k f(t) \ dt \right) $$

$$ \int_{1}^{2} f(t) \ dt + \int_{2}^{3} f(t) \ dt \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \int_{n - 1}^{n} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \int_{0}^{1} f(t) \ dt + \int_{1}^{2} f(t) \ dt \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \int_{n}^{n + 1} f(t) \ dt $$

On peut utiliser la relation de Chasles pour regrouper les termes :

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

Alors, on peut encadrer une série par deux intégrales pour en obtenir une approximation, tel que :

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

$$ (\text{avec } u_n = f(n)) $$

Séries alternées

Critère spécial des séries alternées

Soit $(u_n)_{n \in \mathbb{N}^*}$ une suite décroissante à termes positifs avec :

$$ \lim_{n \to \infty} u_n = 0 $$

De même, soit $A_n$ sa série associée, alternativement positive et négative :

$$ A_n = \sum_{k = 1}^n \Bigl[ (-1)^{k + 1} \ u_k \Bigr] = u_1 - u_2 + u_3 - u_4 \hspace{0.2em} ... $$

Alors, la somme des $2n$ termes peut s'écrire :

$$ A_{2n} = u_1 - u_2 + u_3 - u_4 \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{2n - 1} - u _{2n} $$

On peut regrouper les termes de la façon suivante :

$$ A_{2n} = \underbrace{(u_1 - u_2)} _{\geqslant 0} + \underbrace{(u_3 - u_4)} _{\geqslant 0} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \underbrace{(u_{2n - 1} - u _{2n})} _{\geqslant 0} \qquad(3) $$

Comme la suite est décroissante par hypothèse, les termes mis en évidence entre parenthèses sont tous positifs. La série $(A_n)$ est donc croissante.

Par ailleurs, en présentant $(A_n)$ sous la forme $(3')$, on s'aperçoit que la suite $(A_{2n})$ est toujours inférieur à $u_1$ :

$$ A_{2n} = u_1 - \underbrace{(u_2 - u_3)} _{\geqslant 0} - \underbrace{(u_4 - u_5)} _{\geqslant 0} \hspace{0.2em} - \hspace{0.2em} ... \hspace{0.2em} - \hspace{0.2em} \underbrace{u_{2n}} _{\geqslant 0} \qquad(3') $$

Par conséquent, $(A_n)$ étant croissante et majorée par $u_1$, elle converge est n'excède jamais valeur.

Alors, pour toute suite décroissante à termes positifs $(u_n)_{n \in \mathbb{N}}$ et sa série alternée $(A_n)$ :

$$ \left[ \lim_{n \to \infty} u_n = 0 \right] \Longrightarrow A_n \text{ converge et } (A_n < u_1) $$

$$ \left(\text{avec } A_n = \sum_{k \geqslant 1} \Bigl[ (-1)^{k + 1} \ u_k \Bigr]\right) $$

Exemples

Exemple de comparaison série-intégrale

On cherche à étudier la converge de la série suivante :

$$ S_n = \sum_{k = 1}^n \frac{1}{k^2} $$

Comme la fonction correspondante :

$$ f(n) = \frac{1}{n^2} $$

est bien positive et décroissante, alors on peut utiliser la méthode de comparaison série-intégrale :

$$ \int_{k}^{k + 1} \frac{dt}{t^2} \leqslant f(k) \leqslant \int_{k - 1}^k \frac{dt}{t^2} \ dt $$

On somme les éléments de $(k = 2)$ jusque $n$ (car on verra juste après que $\displaystyle \int^x f(t) \ dt$ n'est pas définie en $0$):

$$ \int_{2}^{n + 1} \frac{dt}{t^2} \leqslant \sum_{k = 2}^n f(k) \leqslant \int_{1}^n \frac{dt}{t^2} \ dt $$

Cherchons maintenant une primitive de $f$. C'est une primitive usuelle :

$$ \int^x \frac{dt}{t^2} = -\frac{1}{t}$$

Soit en remplaçant :

$$ \left[ -\frac{1}{t} \right]_2^{n + 1} \leqslant \sum_{k = 2}^n f(k) \leqslant \left[ -\frac{1}{t} \right]_1^{n} $$

On ajoute $f(1)$ manuellement pour obtenir la somme complète :

$$ f(1) + \left[ -\frac{1}{t} \right]_2^{n + 1} \leqslant \sum_{k = 1}^n f(k) \leqslant f(1) + \left[ -\frac{1}{t} \right]_1^{n} $$

$$ 1 -\frac{1}{n + 1} + \frac{1}{2} \leqslant \sum_{k = 1}^n f(k) \leqslant 1 -\frac{1}{n} + 1 $$

$$ \frac{3}{2} -\frac{1}{n + 1} \leqslant S_n \leqslant 2 -\frac{1}{n} $$

Et on peut à présent tout faire tendre vers l'infini.

$$ \lim_{n \to +\infty} \left[ \frac{3}{2} -\frac{1}{n + 1} \right] \leqslant \lim_{n \to +\infty} \bigl[ S_n \bigr] \leqslant \lim_{n \to +\infty} \left[ 2 -\frac{1}{n} \right] $$

$$ \frac{3}{2} \leqslant \lim_{n \to +\infty} \bigl[ S_n \bigr] \leqslant 2 $$

Cette série est bien convergente car elle est bornée.

Retour en haut de page

Les critères de convergence des séries

Démonstrations

Exemples

Exemple de comparaison série-intégrale