La résolution d'équations du troisième degré (équation cubique)

Une équation du troisième degré est de la forme :

Existence de racine(s) évidente(s)

S'il existe une ou plusieurs racines évidentes, alors on peut factoriser le polynôme et le réduire à un degré inférieur.

Détermination du nombre de racines réelles selon les cas

Après calcul du discriminant \(\Delta_3\) :

On a le nombre de racines réelles suivantes selon les cas :

Résolution

1. si \( (\Delta_3 > 0) \)

• une racine réelle simple

$$ X_1 = \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

• deux racines complexes

$$ C_2 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ C_3 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

Et \( P_3(X) \) se factorise de la sorte :

$$ P_3(X) = a(X - X_1)(X - C_2)(X - C_3) $$

2. si \( (\Delta_3 = 0) \)

• une racine réelle simple

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

• une racine réelle double

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

Et \( P_3(X) \) se factorise de la sorte :

$$ P_3(X) = a(X - X_1)(X - X_2)^2 $$

3. si \( (\Delta_3 < 0) \)

• trois racines réelles

$$ X_1 = \sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + \sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$

Même si elles apparaissent sous forme complexe, après la résolution ces solutions deviennent bien réelles.

Et \( P_3(X) \) se factorise de la sorte :

$$ P_3(X) = a(X - X_1)(X - X_2)(X - X_3) $$

---

Démonstration

Une équation du troisième degré est de la forme :

Alors, on cherche à résoudre :

Existence de racine(s) évidente(s)

S'il existe une ou plusieurs racines évidentes, alors on peut factoriser le polynôme et le réduire à un degré inférieur.

Détermination du nombre de racines réelles selon les cas

Dans le cas général, on peut par une approche graphique, déterminer le nombre de racines selon les cas.

On démarre de l'équation \( (1) \) :

On factorise par \( a \) :

À partir de ce point, on gardera en tête que la forme générale \((2)\) contient \(a\) comme facteur, mais nous allons étudier la fonction l'intérieur de la parenthèse :

On cherche ensuite à éliminer le terme du second degré.

L'expression \((2^*)\) devient alors :

On étudiera alors la fonction \((f)\) :

Remarquons dès à présent que \(f\) est une fonction impaire, étant la somme de fonctions impaires.

Ensuite, cherchons à dériver cette fonction :

Factorisons cette dérivée \(f'\).

Et Cherchons ces racines :

Soient deux racines :

Alors, on peut réécrire sous sa forme factorisée :

Comme la fonction \(f\) change de sens de variations avant \(\chi_1\) et après \(\chi_2\), elle possède donc deux points d'inflexion en \(\chi_1\) et \(\chi_2\).

Et comme on sait que \( P_3(\chi)\) vaut :

Le tableau de variations de \(P_3(\chi)\) sera celui de \(f(\chi)\) si \((a > 0)\), mais sera inversé si \((a < 0)\).

Cherchons les valeurs des images \( f\left(\chi_1 \right) \) et \( f\left(\chi_2 \right) \) :

Pour connaître le nombre de racines de \(f(\chi)\), on cherche à savoir le signe à un instant donné du produit de ces deux images.

qu'on appellera discriminant du troisième degré \(\Delta_3\) :

On aura alors trois sous-cas à envisager :

• \( \alpha) \) si \(\Delta_3 > 0 \)

Si le discriminant est positif, cela signifie que \(f\left(\chi_1\right)\) et \(f\left(\chi_2\right)\) sont de même signe, donc :

• soit tous deux positifs

D'après le tableau de variations de \(f\), il n'y aura qu'une seule racine réelle, située entre \((\chi = -\infty)\) et \((\chi = \chi_1)\).

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$		$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$		$$ \textcolor{#4A8051}{f(\chi_2) > 0} $$		$$ + \infty $$


• soit tous deux négatifs

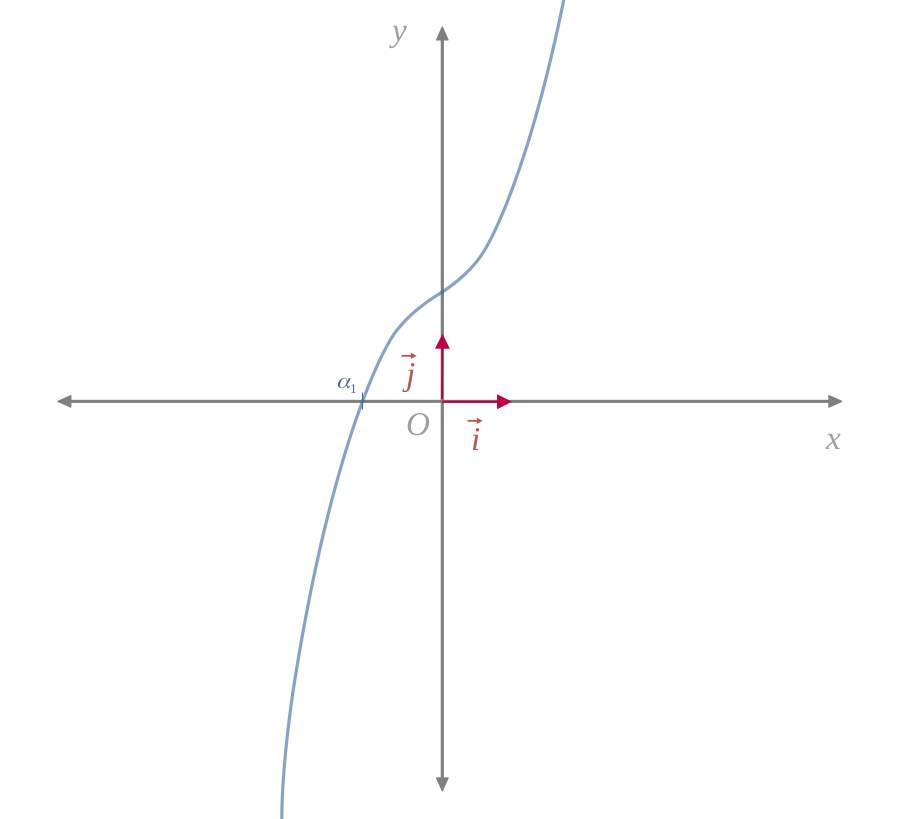
D'après le tableau de variations de \(f\), il n'y aura qu'une seule racine réelle, située entre \((\chi = \chi_2)\) et \((\chi = +\infty)\).

$$ \chi $$	$$ -\infty $$		$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$		$$ \textcolor{#A45959}{f(\chi_1) < 0} $$		$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ + \infty $$

Dans les deux cas, il n'y aura qu'une seule racine réelle.

• \( \beta) \) si \( \Delta_3 = 0 \)

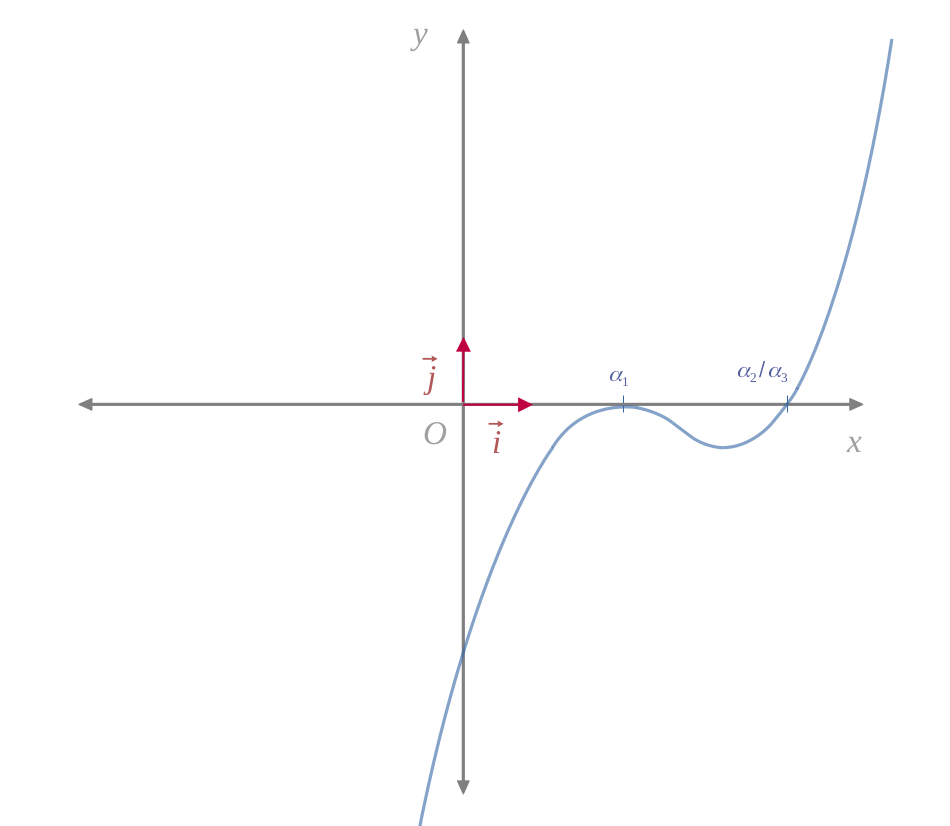
Si le discriminant est nul, cela signifie qu'une des deux images est nulle, car d'après le tableau de variations, on a toujours :

$$ f(\chi_1) > f(\chi_2) $$
• \( f(\chi_1) = 0 \)

Dans ce cas, il y aura une racine double pour \((\chi = \chi_1)\), et une autre pour \((\chi_2 < \chi < +\infty)\).

$$ \chi $$	$$ -\infty $$		$$ \textcolor{#6187B2}{\alpha_1 / \alpha_2 = \chi_1} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_3} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$		$$ \textcolor{#6187B2}{f(\chi_1) = 0} $$		$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\chi_2) = 0} $$	$$ + \infty $$


• \( f(\chi_2) = 0 \)

Dans ce cas symétrique, il y aura une racine simple pour \((\chi_2 < \chi < +\infty)\), ainsi qu'une racine double pour \((\chi = \chi_1)\).

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \textcolor{#6187B2}{\alpha_2 / \alpha_3 = \chi_2} $$		$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$		$$ \textcolor{#6187B2}{f(\chi_2) = 0} $$		$$ + \infty $$



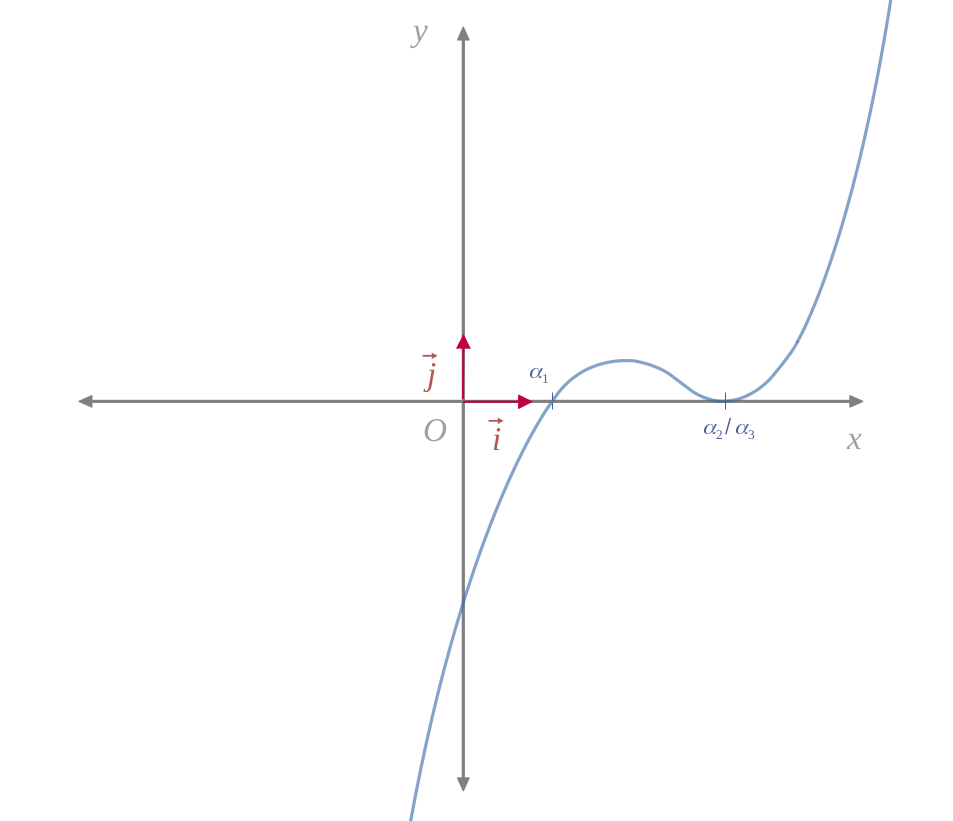
Dans les deux cas, on aura une racine réelle double et une racine réelle simple réelle.

La racine double se situe nécessairement sur le plateau, car dans l'autre cas la fonction est strictement croissante.

• \( \gamma) \) si \( \Delta_3 < 0 \)

Si le discriminant est négatif, les deux images \(f(\chi_1)\) et \(f(\chi_2)\) sont de signes contraires.

Comme on sait que :

$$ f(\chi_1) > f(\chi_2) $$

il n'y a qu'un seul cas, et on distinguera trois racines réelles.

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_2} $$	$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_3} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$	$$ \textcolor{#6187B2}{f(\alpha_2) = 0} $$	$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\alpha_3) = 0} $$	$$ + \infty $$


• \( \delta) \) résumé

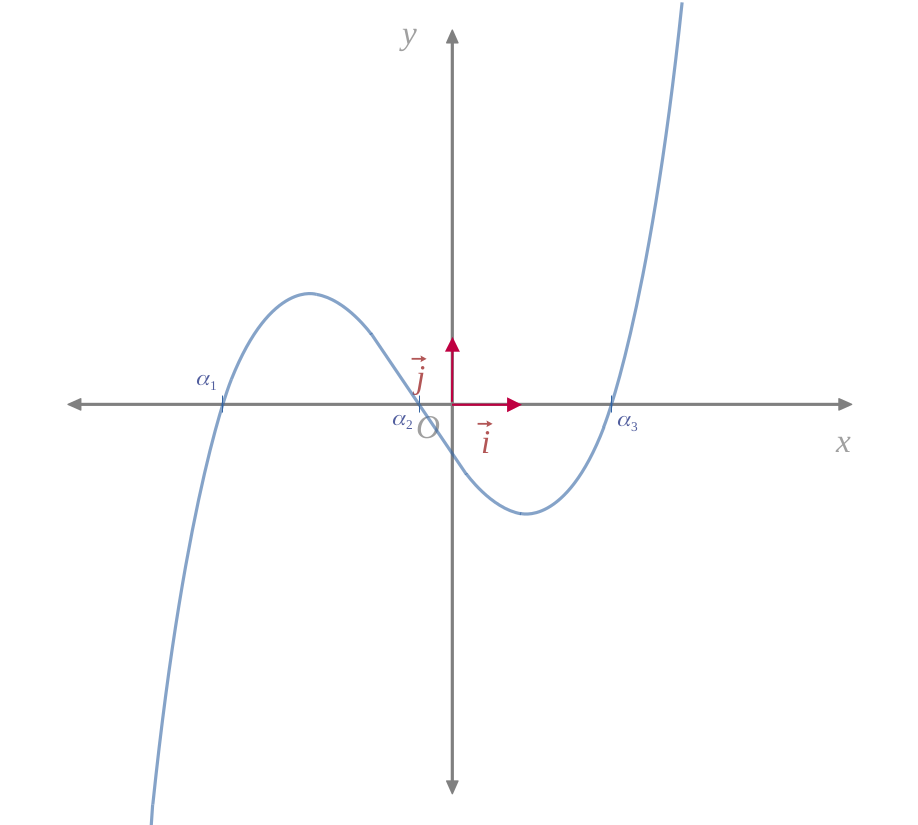
En résumé, voici les cas selon le résultat du discriminant \(( \Delta_3 = q^2 + \frac{4p^3}{27} )\) :

Signe du discriminant \( \Delta_3 \)	Nombres de racines
$$ \Delta_3 > 0 $$	1 racine réelle
$$ \Delta_3 = 0 $$	3 racines réelles (dont une double)
$$ \Delta_3 < 0 $$	3 racine réelles

Résolution

Faisons un bref résumé du cheminement pris dans le point précédent. On a démarré de l'équation à résoudre \((1)\) :

Puis on a factorisé par \(a\) :

Le \(a\) en facteur ne changeant pas les racines, on peut s'en débarrasser :

et poser un premier changement de variable.

On est ensuite arrivé à :

Ce qui nous donne :

On développe :

En multipliant maintenant par \(w^3\), on a :

On est à présent rendu à une équation du second degré en posant à nouveau une nouvelle variable :

Alors, l'expression \((4^*)\) devient :

Avec cette équation du second degré, on peut calculer le discriminant du second degré, qu'on appellera comme plus haut \(\Delta_3\) :

1. si \( (\Delta_3 > 0) \)

Avec l'équation \((5)\) :

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

si \( (\Delta_3 > 0) \), on obtient deux solutions réelles :

$$ z_1 / z_2 = \frac{- q \pm \ \sqrt{\Delta_3}}{2} $$
$$ \Bigl(avec \ \Delta_3 = q^2 + \frac{4p^3}{27} \Bigr) $$

Que l'on peut arranger en :

$$ z_1 / z_2 = -\frac{q}{2} \pm \frac{ \sqrt{q^2 + \frac{4p^3}{27}}}{2} $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \frac{ \sqrt{q^2 + \frac{4p^3}{27}}}{\sqrt{4}} $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \sqrt{\frac{q^2}{4} + \frac{p^3}{27} } $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } $$

Nous avons effectué ces différents changements de variable à la suite :

$$ \left[ X = \chi - \frac{b}{3a} \right] \ puis \ \biggl[ \chi = w - \frac{p}{3w} \biggr] \ puis \ \Bigl[ w^3 = z \Bigr] $$

Il faut donc les remonter en sens inverse :

$$ \Bigl[ z \longmapsto w \Bigr] \ puis \ \Bigl[ w \longmapsto \chi \Bigr] \ puis \ \Bigl[ \chi \longmapsto X \Bigr] $$
1. \(z \longmapsto w \)

En prenant la racine cubique de \(z\), on aura en coefficient les trois racines de l'unité d'un nombre complexe qui sont \( \Bigl \{1, \ e^{\frac{2i\pi}{3}}, \ e^{-\frac{2i\pi}{3}} \Bigr \} \), ce qui nous fait six racines en tout :

$$ w_1 / w_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ w_3 / w_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ w_5 / w_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
2. \(w \longmapsto \chi \)

Les six expressions deviennent alors :

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$
$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3 e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3 e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$

Ensuite, on multiplie les numérateurs et dénominateurs par leurs conjugués respectfifs.

Pour le premier couple de solutions \(\chi_1 / \chi_2 \) :

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} }{3\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 - \left(\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right) } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{\underbrace{\left(\frac{q}{2} \right)^2 - \left(\frac{q}{2}\right)^2 } _\text{= 0} - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{ \left(- \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{-\frac{3p}{3}} $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

Ces deux racines sont en réalité une seule, à cause des doubles signes \(\pm\) et \(\mp \) présents dans chacun des deux premiers termes :

$$ \chi_1 = \chi_2 = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

Pour les deux autres couples de soutions \((\chi_3 / \chi_4, \ \chi_5 / \chi_6)\), on suit la même démarche, et on arrive après calculs aux formes suivantes :

$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

Pour eux aussi, on peut les regrouper car elles sont deux-à-deux indentiques :

$$ X_3 = X_6 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ X_4 = X_5 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
3. \(\chi \longmapsto X \)

Pour cette dernière étape, on a juste à ajouter à chaque solution le terme \(-\frac{b}{3a}\).

$$ X_1 = X_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
$$ X_3 = X_6 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
$$ X_4 = X_5 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
4. conclusion

On a vu plus haut l'égalité :

$$ \frac{- q \pm \ \sqrt{\Delta_3}}{2} = -\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } $$

Alors, on remet cette égalité en place pour la présentation des solutions.

On a alors dans ce cas de \( (\Delta_3 > 0) \) :

• une racine réelle simple

$$ X_1 = \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

• deux racines complexes

$$ C_2 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ C_3 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ avec \ \left(\Delta_3 = q^2 + \frac{4p^3}{27} \right) $$
$$ et \ \left \{ \begin{gather*} p = \frac{-b^2 + 3ac}{3a^2} \\ \\ q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \end{gather*} \right \} $$

Ainsi, le polynôme \(P_3(X)\) admet la factorisation :

$$ P_3(X) = a(X - X_1)(X - C_2)(X - C_3) $$
2. si \( (\Delta_3 = 0) \)

Avec l'équation \((5)\) :

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

si \( (\Delta_3 = 0) \), on une solution réelle double :

$$ z_0 = -\frac{q}{2} $$

De la même manière que plus haut, on remonte les différents changements de variable les uns à la suite des autres.

1. \(z \longmapsto w \)
$$ w_1 = \sqrt[3]{-\frac{q}{2}} $$
$$ w_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ w_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
2. \(w \longmapsto \chi \)

Pour la première solution \(\chi_1 \) :

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3\sqrt[3]{-\frac{q}{2}}}$$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3\sqrt[3]{-\frac{q}{2}}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\textcolor{#A45959}{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}}{\sqrt[3]{-\frac{q}{2}} \textcolor{#A45959}{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$

Mais comme :

$$ \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = \frac{\Delta_3}{2} $$

(voir plus haut)

Et que l'on a comme hypothèse que \( \Delta_3 = 0 \), alors :

$$\Delta_3 = 0 \Longrightarrow 2 \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = 0 $$

Et donc que :

$$\sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = 0 $$

Ce qui implique aussi que :

$$\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 = 0 $$

$$\left(\frac{q}{2}\right)^2 = - \left( \frac{p}{3} \right)^3 $$

$$\sqrt[3]{ \left(\frac{q}{2}\right)^2 } = \sqrt[3]{ - \left( \frac{p}{3} \right)^3 } $$

$$\sqrt[3]{ \left(\frac{q}{2}\right)^2 } = -\frac{p}{3} $$

On peut alors remplacer dans l'expression précédente :

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \frac{ \sqrt[3]{ \left(\frac{q}{2}\right)^2 } \sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \frac{ \sqrt[3]{ \left(-\frac{q}{2}\right)^2 } \sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$

À présent, on fait jouer les formules des puissances:

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \left(-\frac{q}{2}\right)^{\frac{4}{3}} \left(-\frac{q}{2}\right)^{-1 } $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \left(-\frac{q}{2}\right)^{\frac{1}{3}} $$
$$ \chi_1 = 2\sqrt[3]{-\frac{q}{2}} $$

Pour les deux autres solutions :

$$ w_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ w_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$

Ces deux solutions sont une seule et même solution :

$$ \chi_2 = \chi_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_2 = \chi_3 = \sqrt[3]{-\frac{q}{2}} \left(e^{\frac{2i\pi}{3}} + e^{-\frac{2i\pi}{3}} \right) $$
$$ \chi_2 = \chi_3 = -\sqrt[3]{-\frac{q}{2}} $$
3. \(\chi \longmapsto X \)
$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
4. conclusion

On a alors dans ce cas de \( (\Delta_3 = 0) \) :

• une racine réelle simple

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

• une racine réelle double

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ avec \ \left(q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \right) $$

Ainsi, le polynôme \(P_3(X)\) admet la factorisation :

$$ P_3(X) = a(X - X_1)(X - X_2)^2 $$
3. si \( (\Delta_3 < 0) \)

Avec l'équation \((5)\) :

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

si \( (\Delta_3 < 0) \), on obtient deux solutions complexes :

$$ z_1 = \frac{- q \pm i\sqrt{|\Delta_3|}}{2} $$

Que l'on peut arranger comme précédemment en :

$$ z_1 / z_2 = -\frac{q}{2} \pm i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| } $$

De la même manière que plus haut, on remonte les différents changements de variable les uns à la suite des autres.

1. \(z \longmapsto w \)
$$ w_1 / w_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ w_3 / w_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ w_5 / w_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
2. \(w \longmapsto \chi \)

Les six expressions deviennent alors :

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$
$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3 e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3 e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$

Pour le premier couple de solutions \(\chi_1 / \chi_2 \) :

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} }{3\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 + \left|\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 + -\left(\frac{q}{2}\right)^2 - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\underbrace{\left(\frac{q}{2} \right)^2 + -\left(\frac{q}{2}\right)^2} _\text{ = 0 } - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{- \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{-\frac{3p}{3}} $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$

Ces deux solutions sont une seule et même solution.

$$ \chi_1 = \chi_2 = \sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$

Pour les deux autres couples de soutions \((\chi_3 / \chi_4, \ \chi_5 / \chi_6)\), on suit la même démarche, et on arrive après calculs aux formes suivantes :

$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
3. \(\chi \longmapsto X \)
$$ X_1 = X_2 = \sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ - i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
$$ \chi_3 = \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
$$ \chi_5 = \chi_6 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
4. conclusion

De la même manière que plus haut, on se débarrasse de la valeur absolue dans la présentation des résultats.

On a alors dans ce cas de \( (\Delta_3 < 0) \) :

• trois racines réelles

$$ X_1 = \sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + \sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ avec \ \left(\Delta_3 = q^2 + \frac{4p^3}{27} \right) $$
$$ et \ \left \{ \begin{gather*} p = \frac{-b^2 + 3ac}{3a^2} \\ \\ q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \end{gather*} \right \} $$

Même si elles apparaissent sous forme complexe, après la résolution ces solutions deviennent bien réelles.

Ainsi, le polynôme \(P_3(X)\) admet la factorisation :

$$ P_3(X) = a(X - X_1)(X - X_2)(X - X_3) $$

---

Exemples

1. Existence de racine(s) évidente(s)

$$ P_3(X) = X^3 + X^2 + X + 1 $$

On remarque que \( (X = -1) \) est une racine évidente. Cherchons alors le polynôme du second degré munis des coefficients \((\alpha, \beta, \gamma)\) tels que :

$$ P_3(X) = (X + 1)(\alpha X^2 + \beta X + \gamma) $$

Faisons une division pour déterminer ce polynôme :

$$$$	$$ X + 1 $$
$$\hspace{1em} X^3 + X^2 + X + 1 $$	$$ \textcolor{#608742}{X^2} $$
$$ \textcolor{#AF5F5F}{-X^3} \textcolor{#AF5F5F}{-X^2} + X + 1 $$	$$ X^2 $$
$$ \hspace{1em} 0 \hspace{1.2em} + \hspace{0.2em} 0 \hspace{0.4em} \textcolor{#AF5F5F}{-X - 1} $$	$$ X^2 \textcolor{#608742}{+ 1} $$

Alors,

$$ P_3(X) = (X + 1)(X^2 + 1) $$

On cherche maintenant ces racines.

$$ \Delta = 0^2 - 4 \times 1 \times 1$$
$$ \Delta = -4 $$

Comme \(\Delta\) est négatif, il y a deux racines complexes :

$$ C_1 = \frac{- 0 - i\sqrt{-(-4)}}{2 \times 1} $$
$$ C_1 = -i $$
$$ C_2 = \frac{- 0 + i\sqrt{-(-4)}}{2 \times 1} $$
$$ C_2 = i $$

Alors, les trois solutions pour \( \Bigl[ P_3(X) = 0 \Bigr] \) sont :

$$ \mathcal{S} = \biggl \{X_{1} = -1 , \ C_{2} = -i, \ C_{3} = i \biggr \} $$

\(P_3(X) \) peut alors se factoriser :

$$ P_3(X) = (X + 1)(X + i)(X - i) $$

2. Cas d'un discrimant nul

$$ R_3(X) = X^3 - 5X^2 + 8X - 4 $$

On calcule le discriminant du troisième degré :

$$ \Delta_3 = q^2 + \frac{4p^3}{27}$$
$$ \Delta_3 = \left(\frac{2b^3 + 27a^2d - 9abc}{27a^3}\right)^2 + \frac{4\left(\frac{-b^2 + 3ac}{3a^2}\right)^3}{27} $$
$$ \Delta_3 = 0 $$

Comme \(\Delta\) est nul, on a trois racines réelles :

• une racine réelle simple

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_1 = 1 $$

• une racine réelle double

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_2 = X_3 = 2 $$

\(R_3(X) \) peut alors se factoriser :

$$ R_3(X) = (X - 1)(X - 2)^2 $$