The derivatives of trigonometric functions
For all these trigonometric functions, we will also have their respective reciprocal function.
Between a function and its reciprocal function, we do have the following relation:
$$ f \circ f^{-1} = id$$
Here is an example with \(sin(x)\) and \(arcsin(x)\) :
$$ \Biggl \{ \begin{gather*}
f : x \longmapsto sin(x), \hspace{3.1em} \mathbb{R } \longmapsto [-1, \enspace 1] \\
f^{-1} : x \longmapsto arcsin(x), \enspace [-1, \enspace 1] \longmapsto \mathbb{R } \end{gather*} $$
$$ arcsin(sin(x)) = x \Longleftrightarrow sin(arcsin(x)) = x $$
Be careful not to be confused with the notation "\( f^{-1} \)" of reciprocal functions with that of an inverse.
Indeed, we note "\( cos^{-1}, \ sin^{-1}, \ tan^{-1}... \)" for trigonometric reciprocal functions \( (arcsin, \ arccos, \ arctan...) \), but this is a different notation from "\( f^{-1} \)" which generally means the inverse function \( (x^{-1} = \frac{1}{x}) \).
$$ cos^2(x) = cos(x)cos(x) $$
$$ (but) $$
$$ \Biggl[ cos^{-1}(x) = arccos(x) \Biggr] \ \neq \ \Biggl[ \Bigl(cos(x)\Bigr)^{-1} = \frac{1}{cos(x)} = sec(x) \Biggr] $$
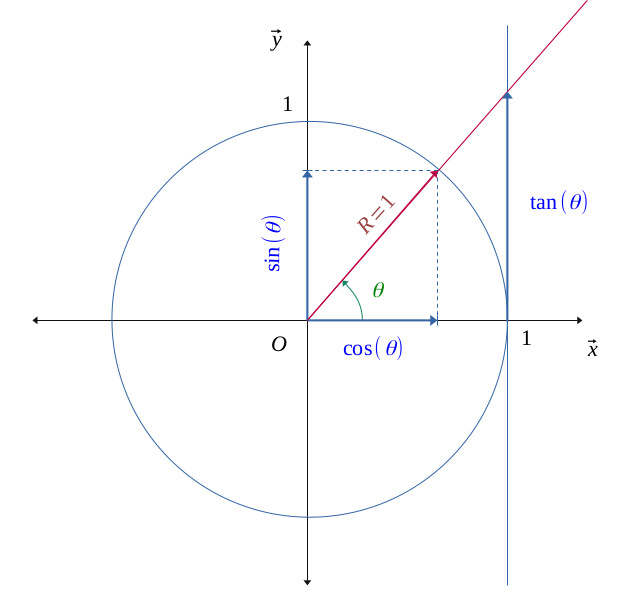
Applying the Thales' theorem, we definitely see the following relation:
$$ \frac{cos(\theta)}{1} = \frac{sin(\theta)}{tan(\theta)} \Longleftrightarrow tan(\theta) = \frac{sin(\theta)}{cos(\theta)} $$
The \( sin(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sin(x) $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ sin(x)' = cos(x) $$
The \( cos(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = cos(x) $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ cos(x)' = -sin(x) $$
The \( tan(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = tan(x) = \frac{sin(x)}{cos(x)} $$
Its derivative is:
$$ \forall k \in \mathbb{Z}, \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr] $$
$$ tan(x)' = 1 + tan^2(x) = \frac{1}{cos^2(x)}= sec^2(x) $$
The \( arcsin(x) \) is the reciprocal function of the \( sin(x) \) function, it is defined as follows:
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arcsin(x) = sin^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-1 ,\hspace{0.2em} 1[, $$
$$ arcsin(x)' = \frac{1}{\sqrt{1 - x^2}} $$
The \( arccos(x) \) function is the reciprocal function of the \( cos(x) \) function, it is defined as follows:
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arccos(x) = cos^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-1 , \hspace{0.2em}1[, $$
$$ arccos(x)' = -\frac{1}{\sqrt{1 - x^2}} $$
The \( arctan(x) \) function is the reciprocal function of the \( tan(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = arctan(x) = tan^{-1}(x) $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ arctan(x)' = \frac{1}{1 + x^2} $$
The three secant trigonometric functions are the \( cosec(x), sec(x) \) and \( cotan(x) \) functions.
They are respectively the inverses of the \( sin(x), cos(x) \) and \( tan(x) \) functions.
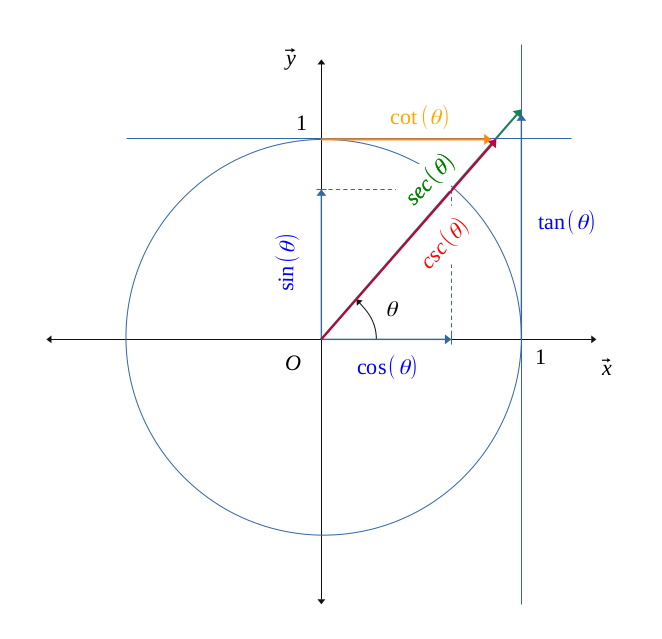
Applying the Thales' theorem, we definitely see the following relation:
$$ \left \{ \begin{gather*}
\frac{cosec(\theta)}{1} = \frac{1}{sin(\theta)} \Longleftrightarrow cosec(\theta) = \frac{1}{sin(\theta)} \\
\frac{sec(\theta)}{1} = \frac{1}{cos(\theta)} \Longleftrightarrow sec(\theta) = \frac{1}{cos(\theta)} \\
\frac{cotan(\theta)}{1} = \frac{cosec(\theta)}{sec(\theta)} = \frac{1}{tan(\theta)} \Longleftrightarrow cotan(\theta) = \frac{1}{tan(\theta)}
\end{gather*} \right \} $$
The \( cosec(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], \enspace f(x) = cosec(x) = \frac{1}{sin(x)} $$
Its derivative is:
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cosec(x)' = - cosec^2(x)cos(x) = -cosec(x)cotan(x) $$
Furthermore, we do notice that:
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ \frac{cosec'(x)}{cosec(x)} = -cosec(x)cos(x) = -tan(x)$$
The \( sec(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = sec(x) = \frac{1}{cos(x)} $$
Its derivative is:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ sec(x)' = sec^2(x) sin(x) = sec(x)tan(x) $$
Furthermore, we do notice that:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ \frac{sec'(x)}{sec(x)} = sec(x)sin(x) = tan(x)$$
The \( cotan(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr] , \enspace f(x) = cotan(x) = \frac{cosec(x)}{sec(x)} = \frac{1}{tan(x)} $$
Its derivative is:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cotan(x)' = -(1 + cotan^2(x)) = - cosec^2(x) $$
The \( arccosec(x) \) is the reciprocal function of the \( cosec(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccosec(x) = cosec^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
The \( arcsec(x) \) is the reciprocal function of the \( sec(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arcsec(x) = sec^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arcsec(x)' = \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
The \( arccotan(x) \) is the reciprocal function of the \( cotan(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R} , \enspace f(x) = arccotan(x) = cotan^{-1}(x) $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ arccotan(x)' = - \frac{1}{ 1 + x^2} $$
The three hyperbolic functions are the \( sinh(x), cosh(x) \) and \( tanh(x) \) functions.
They are the twins of the \( sin(x), cos(x) \) and \( tan(x) \) functions, and notably concerning their properties.
The \( sinh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sinh(x) = \frac{e^x - e^{-x} }{2} $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ sinh(x)' = cosh(x) $$
The \( cosh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = cosh(x) = \frac{e^x + e^{-x} }{2} $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ cosh(x)' = sinh(x) $$
The \( tanh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = tanh(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ tanh(x)' = 1 - tanh^2(x) = sech^2(x) $$
The \( arcsinh(x) \) is the reciprocal function of the \( sinh(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = arcsinh(x)= sinh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in \mathbb{R},$$
$$ arcsinh(x) = ln \left|x + \sqrt{x^2 + 1}\right| $$
(\(\Longrightarrow\) see demonstration of it)
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + x^2}} $$
The \( arccosh(x) \) is the reciprocal function of the \( cosh(x) \) function, it is defined as follows:
$$ \forall x \in [1, \hspace{0.1em} +\infty[, \enspace f(x) = arccosh(x) = cosh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x) = ln \Bigl| x + \sqrt{x^2 - 1}\Bigr| $$
(\(\Longrightarrow\) see demonstration of it)
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x)' = \frac{1}{\sqrt{x^2 -1}} $$
The \( arctanh(x) \) is the reciprocal function of the \( tanh(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, \enspace f(x) = arctanh(x) = tanh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x) = \frac{1}{2} ln \left| \frac{1 + x}{1 - x} \right| $$
(\(\Longrightarrow\) see demonstration of it)
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x)' = \frac{1}{1 - x^2} $$
The three hyperbolic secant functions are the \( cosech(x), sech(x) \) and \( cotanh(x) \) functions.
They are respectively the inverses of the \( sinh(x), cosh(x) \) and \( tanh(x) \) functions.
The \( cosech(x) \) function is defined as follows:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cosech(x) = \frac{1}{sinh(x)} $$
Its derivative is:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cosech(x)' = - cosech^2(x) cosh(x) = -cosech(x)cotanh(x) $$
Furthermore, we do notice that:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ \frac{cosech'(x)}{cosech(x)} = -cosech(x)cosh(x) = -cotanh(x)$$
The \( sech(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sech(x) = \frac{1}{cosh(x)} $$
Its derivative is:
$$ \forall x \in \mathbb{R}, $$
$$ sech(x)' = -sech^2(x)sinh(x) = -sech(x)tanh(x) $$
The \( cotanh(x) \) function is defined as follows:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cotanh(x) = \frac{1}{tanh(x)} $$
Its derivative is:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cotanh(x)' = 1 - cotan^2(x) = -cosech^2(x)$$
The \( arccosech(x) \) is the reciprocal function of the \( cosech(x) \) function, it is defined as follows:
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , \enspace f(x) = arccosech(x) = cosech^{-1}(x) $$
Its derivative is:
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , $$
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 + \frac{1}{ x^2}}} $$
The \( arcsech(x) \) is the reciprocal function of the \( sech(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]0, \hspace{0.1em} 1] , \enspace f(x) = arcsech(x) = sech^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.1em} ]0, \hspace{0.1em} 1], $$
$$ arcsech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{\frac{1}{ x^2} - 1}} $$
The \( arccotanh(x) \) is the reciprocal function of the \( cotanh(x) \) function, it is defined as follows:
$$ \forall \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccotanh(x) =cotanh^{-1}(x) $$
Its derivative is:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccotanh(x)' = \frac{1}{ 1 - x^2} $$
Click on the title to access to the recap table.
Demonstrations
The \( sin(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sin(x) $$
With the definition of the derivative, we do have:
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x + h) - sin(x)}{h} $$
We know from the trigonometric addition formulas that:
$$ \forall (\alpha, \beta) \in \hspace{0.04em} \mathbb{R}^2, $$
$$ sin(\alpha + \beta) = sin(\alpha) cos(\beta) + cos(\alpha) sin(\beta) $$
So:
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x) cos(h) + cos(x) sin(h) - sin(x)}{h} $$
When \( h \to 0\), \( cos(h) \to 1\) and \( sin(h) \to h\).
Then,
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{ sin(x) + cos(x). h - sin(x)}{h} $$
$$ sin(x)' = \lim_{h \to 0 } \enspace \frac{cos(x). h }{h} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ sin(x)' = cos(x) $$
The \( cos(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = cos(x) $$
With the definition of the derivative, we do have:
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x + h) - cos(x)}{h} $$
We know from the trigonometric addition formulas that:
$$ \forall (\alpha, \beta) \in \hspace{0.04em} \mathbb{R}^2, $$
$$ cos(\alpha + \beta) = cos(\alpha) cos(\beta) - sin(\alpha) sin(\beta) $$
So:
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x) cos(h) - sin(x) sin(h) - cos(x)}{h} $$
When \( h \to 0\), \( cos(h) \to 1\) and \( sin(h) \to h\).
Then,
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ cos(x) - sin(x). h - cos(x)}{h} $$
$$cos(x)' = \lim_{h \to 0 } \enspace \frac{ - sin(x). h }{h} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ cos(x)' = -sin(x) $$
The \( tan(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = tan(x) = \frac{sin(x)}{cos(x)} $$
By definition:
$$ tan(x)' = \left( \frac{sin(x)}{cos(x)} \right)' $$
So in our case:
$$ tan(x)' = \frac{cos(x)cos(x) + sin(x)sin(x)}{cos^2(x)} $$
$$ tan(x)' = \frac{cos^2(x) + sin^2(x)}{cos^2(x)} $$
$$ tan(x)' = \frac{cos^2(x) + sin^2(x)}{cos^2(x)} $$
And finally we do have,
$$ \forall k \in \mathbb{Z}, \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr] $$
$$ tan(x)' = 1 + tan^2(x) = \frac{1}{cos^2(x)} = sec^2(x) $$
The \( arcsin(x) \) is the reciprocal function of the \( sin(x) \) function, it is defined as follows:
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arcsin(x) = sin^{-1}(x) $$
We can calculate this derivative using the derivative of a reciprocal function :
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = sin(x) \\
f'(x) = cos(x) \\
f^{-1}(x) = arcsin(x) \end{gather*} \right \} $$
Consequently,
$$ arcsin(x)' = \frac{1}{cos(arcsin(x))} $$
Furthermore,
$$ cos^2(x) + sin^2(x) = 1$$
$$ cos^2(x) = 1 - sin^2(x) $$
$$ | cos(x) | = \sqrt{1 - sin^2(x)} $$
But, the \(arcsin(x)\) function being defined when \( x \in \bigl[-1; 1\bigr]\) with values in \(\left[-\frac{\pi}{2}; \frac{\pi}{2} \right]\), the \(cos(arcsin(x))\) function is always positive because the \(cos(X)\) function is positive when \(X \in \left[-\frac{\pi}{2}; \frac{\pi}{2} \right]\).
$$x \longmapsto arcsin(x)$$
$$\bigl[-1; 1\bigr] \longmapsto \left[-\frac{\pi}{2}; \frac{\pi}{2} \right]$$
$$ \hspace{12em} X \longmapsto cos(X)$$
$$\hspace{12em} \left[-\frac{\pi}{2}; \frac{\pi}{2} \right] \longmapsto \bigl[0; 1\bigr]$$
So in our case, when can keep only the positive case:
$$ cos(arcsin(x)) = \sqrt{1 - sin^2(arcsin(x))} $$
Thus, replacing it, we do have,
$$ arcsin(x)' = \frac{1}{\sqrt{1 - sin^2(arcsin(x))}} $$
And as a result,
$$ \forall x \in \hspace{0.04em} ]-1 ,\hspace{0.2em} 1[, $$
$$ arcsin(x)' = \frac{1}{\sqrt{1 - x^2}} $$
The \( arccos(x) \) function is the reciprocal function of the \( cos(x) \) function, it is defined as follows:
$$ \forall x \in [-1, \hspace{0.2em} 1], \enspace f(x) = arccos(x) = cos^{-1}(x) $$
By the same reasoning as before with \(arcsin(x)'\) calculation:
$$ arccos(x)' = - \frac{1}{\sqrt{1 - cos^2(arccos(x))}} $$
And finally,
$$ \forall x \in \hspace{0.04em} ]-1 , \hspace{0.2em}1[, $$
$$ arccos(x)' = -\frac{1}{\sqrt{1 - x^2}} $$
The \( arctan(x) \) function is the reciprocal function of the \( tan(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = arctan(x) = tan^{-1}(x) $$
By the same reasoning as before with \(arcsin(x)'\) calculation:
$$ arctan(x)' = \frac{1}{1 + tan^2(arctan(x))} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ arctan(x)' = \frac{1}{1 + x^2} $$
The \( cosec(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z},\ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], \enspace f(x) = cosec(x) = \frac{1}{sin(x)} $$
By definition:
$$ cosec(x)' = \biggl(\frac{1}{sin(x)} \biggr)' $$
So in our case,
$$ cosec(x)' = -\frac{cos(x)}{sin^2(x)} $$
And finally,
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cosec(x)' = - cosec^2(x)cos(x) = -cosec(x)cotan(x)$$
Furthermore, we do notice that:
$$ \frac{cosec'(x)}{cosec(x)} = \frac{-cosec^2(x)cos(x)}{cosec(x)} $$
$$ \forall k \in \mathbb{Z}, \ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ \frac{cosec'(x)}{cosec(x)} = -cosec(x)cos(x) = -tan(x)$$
The \( sec(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], \enspace f(x) = sec(x) = \frac{1}{cos(x)} $$
By definition:
$$ sec(x)' = \biggl(\frac{1}{cos(x)} \biggr)' $$
We apply again the inverse of a function's derivative:
$$ sec(x)' = \frac{sin(x)}{cos^2(x)} $$
And finally,
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ sec(x)' = sec^2(x) sin(x) = sec(x)tan(x) $$
Furthermore, we do notice that:
$$ \frac{sec'(x)}{sec(x)} = \frac{sec^2(x)tan(x)}{sec(x)} $$
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \biggl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \Bigl \{ \frac{\pi}{2} + k\pi \Bigr \} \biggr], $$
$$ \frac{sec'(x)}{sec(x)} = sec(x)sin(x) = tan(x)$$
The \( cotan(x) \) function is defined as follows:
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr] , \enspace f(x) = cotan(x) = \frac{cosec(x)}{sec(x)} = \frac{1}{tan(x)} $$
By definition:
$$ cotan(x)' = \biggl(\frac{1}{tan(x)} \biggr)' $$
We apply again the inverse of a function's derivative:
$$ cotan(x)' = - \frac{1 + tan^2(x)}{tan^2(x)} $$
And finally,
$$ \forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ k\pi \bigr \} \Bigr], $$
$$ cotan(x)' = -(1 + cotan^2(x)) = - cosec^2(x) $$
The \( arccosec(x) \) is the reciprocal function of the \( cosec(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccosec(x) = cosec^{-1}(x) $$
We can calculate this derivative using the derivative of a reciprocal function:
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = cosec(x) \\
f'(x) = - cosec^2(x)cos(x) \\
f^{-1}(x) = arccosec(x) \end{gather*} \right \} $$
$$ arccosec(x)' = -\frac{1}{cosec^2(arccosec(x)) \times cos(arccosec(x))} $$
Furthermore,
$$ cos^2(x) + sin^2(x) = 1$$
$$ cos^2(x) = 1 - sin^2(x) $$
$$ | cos(x) | = \sqrt{1 - sin^2(x)} $$
But, the \(arccosec(x)\) function is defined when \( x \in \bigl[-\infty; -1\bigr] \cup \bigl[1; +\infty\bigr] \) with values in \(\left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \), the \(cos(arcsin(x))\) function is always positive because the \(cos(X)\) function is positive when \( X \in \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \).
$$\hspace{6em} x \longmapsto arccosec(x)$$
$$\bigl[-\infty; -1\bigr] \cup \bigl[1; +\infty\bigr] \longmapsto \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right]$$
$$ \hspace{16em} X \longmapsto cos(X)$$
$$\hspace{16em} \left[-\frac{\pi}{2}; 0 \right[ \cup \left]0; \frac{\pi}{2} \right] \longmapsto \bigl[0; 1\bigr]$$
So in our case, when can keep only the positive case:
$$ cos(arccosec(x)) = \sqrt{1 - sin^2(arccosec(x))} $$
$$ arccosec(x)' = -\frac{1}{cosec^2(arccosec(x)) \times \sqrt{1 - sin^2(arccosec(x))}} $$
But:
$$ cosec(x) = \frac{1}{sin(x)} \Longleftrightarrow sin(x) = \frac{1}{cosec(x)} $$
So,
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{cosec^2(arccosec(x))}}} $$
Soit finalement,
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arccosec(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
The \( arcsec(x) \) is the reciprocal function of the \( sec(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1] \cup[1, \hspace{0.1em} +\infty[ , \enspace f(x) = arcsec(x) = sec^{-1}(x) $$
By the same reasoning as before with \(arccosec(x)'\) calculation:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[\hspace{0.1em}\cup \hspace{0.1em}]1, \hspace{0.1em} +\infty[, $$
$$ arcsec(x)' = \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 - \frac{1}{ x^2}}} $$
The \( arccotan(x) \) is the reciprocal function of the \( cotan(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R} , \enspace f(x) = arccotan(x) = cotan^{-1}(x) $$
By the same reasoning as before with \(arccosec(x)'\) calculation:
$$ \forall x \in \mathbb{R}, $$
$$ arccotan(x)' = - \frac{1}{ 1 + x^2} $$
The \( sinh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sinh(x) = \frac{e^x - e^{-x} }{2} $$
Here, we will use a chain derivation to derivate exponentials:
$$ sinh(x)' = \biggl(\frac{e^x - e^{-x}}{2} \biggr)' $$
$$ sinh(x)' = \frac{1}{2} \bigl( e^x + e^{-x} \bigr) $$
$$ sinh(x)' = \biggl(\frac{e^x + e^{-x}}{2} \biggr) $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ sinh(x)' = cosh(x) $$
The \( cosh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = cosh(x) = \frac{e^x + e^{-x} }{2} $$
By the same reasoning as before with \(sinh(x)'\) calculation:
$$ cosh(x)' = \biggl(\frac{e^x + e^{-x}}{2} \biggr)' $$
$$ cosh(x)' = \frac{1}{2} \bigl( e^x - e^{-x} \bigr) $$
$$ cosh(x)' = \biggl(\frac{e^x - e^{-x}}{2} \biggr) $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ cosh(x)' = sinh(x) $$
The \( tanh(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = tanh(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
By definition:
$$ tanh(x)' = \biggl(\frac{e^x - e^{-x}}{e^x + e^{-x}} \biggr)' $$
Let us apply the derivative of a quotient:
$$ tanh(x)' = \frac{(e^x + e^{-x}) (e^x + e^{-x}) - (e^x - e^{-x})(e^x - e^{-x})}{(e^x + e^{-x})^2} $$
$$ tanh(x)' = \frac{(e^x + e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2} $$
$$ tanh(x)' = 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ tanh(x)' = 1 - tanh^2(x) = sech^2(x) $$
The \( arcsinh(x) \) is the reciprocal function of the \( sinh(x) \) function, it is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = arcsinh(x)= sinh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in \mathbb{R}, $$
$$ arcsinh(x) = ln \left|x + \sqrt{x^2 + 1}\right| $$
(\(\Longrightarrow\) see demonstration of it)
We can calculate this derivative using the derivative of a reciprocal function:
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ avec \ \left \{ \begin{gather*}
f(x) = sinh(x) \\
f('x) = cosh(x) \\
f^{-1}(x) = arcsinh(x) \end{gather*} \right \} $$
$$ arcsinh(x)' = \frac{1}{cosh(arcsinh(x))} $$
Furthermore,
$$ cosh^2(x) -sinh^2(x) = 1$$
$$ cosh^2(x) = 1 + sinh^2(x) $$
$$ | cosh(x) | = \sqrt{1 +sinh^2(x)} $$
Since the \(cosh(x)\) function is always positive when \(x \in \mathbb{R}\), we can keep the positive case:
$$ cosh(x) = \sqrt{1 + sinh^2(x)} $$
So, replacing it we do have :
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + sinh^2(arcsinh(x))}} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ arcsinh(x)' = \frac{1}{\sqrt{1 + x^2}} $$
The \( arccosh(x) \) is the reciprocal function of the \( cosh(x) \) function, it is defined as follows:
$$ \forall x \in [1, \hspace{0.1em} +\infty[, \enspace f(x) = arccosh(x) = cosh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in [1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x) = ln \Bigl| x + \sqrt{x^2 - 1}\Bigr| $$
(\(\Longrightarrow\) see demonstration of it)
By the same reasoning as before with \(arcsinh(x)'\) calculation:
$$ \forall x \in \hspace{0.04em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccosh(x)' = \frac{1}{\sqrt{x^2 -1}} $$
The \( arctanh(x) \) is the reciprocal function of the \( tanh(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, \enspace f(x) = arctanh(x) = tanh^{-1}(x) $$
In addition, we can define it more explicitly by :
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, \forall x \in [1, \hspace{0.1em} +\infty[, $$
$$ \ arctanh(x) = \frac{1}{2} ln \left| \frac{1 + x}{1 - x} \right| $$
(\(\Longrightarrow\) see demonstration of it)
By the same reasoning as before with \(arcsinh(x)'\) calculation:
$$ \forall x \in \hspace{0.04em} ]-1, \hspace{0.1em} 1[, $$
$$ arctanh(x)' = \frac{1}{1 - x^2} $$
The \( cosech(x) \) function is defined as follows:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cosech(x) = \frac{1}{sinh(x)} $$
By definition:
$$ cosech(x)' = \biggl(\frac{1}{sinh(x)} \biggr)' $$
So in our case,
$$ cosech(x)' = -\frac{cosh(x)}{sinh^2(x)} $$
And finally,
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cosech(x)' = - cosech^2(x) cosh(x) = -cosech(x)cotanh(x) $$
Furthermore, we do notice that:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ \frac{cosech'(x)}{cosech(x)} = -cosech(x)cosh(x) = -cotanh(x)$$
The \( sech(x) \) function is defined as follows:
$$ \forall x \in \mathbb{R}, \enspace f(x) = sech(x) = \frac{1}{cosh(x)} $$
By definition:
$$ sech(x)' = \biggl(\frac{1}{cosh(x)} \biggr)' $$
We apply again the inverse of a function's derivative:
$$ sech(x)' = -\frac{sinh(x)}{cosh^2(x)} $$
And finally,
$$ \forall x \in \mathbb{R}, $$
$$ sech(x)' = -sech^2(x)sinh(x) = -sech(x)tanh(x) $$
Furthermore, we do notice that:
$$ \forall x \in \mathbb{R}, $$
$$ \frac{sech'(x)}{sech(x)} = -sech(x)sinh(x) = -tanh(x)$$
The \( cotanh(x) \) function is defined as follows:
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], \enspace f(x) = cotanh(x) = \frac{1}{tanh(x)} $$
By definition:
$$ cotanh(x)' = \biggl(\frac{1}{tanh(x)} \biggr)' $$
We apply again the inverse of a function's derivative:
$$ cotanh(x)' = - \frac{1 - tanh^2(x)}{tanh^2(x)} $$
And as a result,
$$ \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \hspace{0.2em} \bigl \{ 0 \bigr \} \Bigr], $$
$$ cotanh(x)' = 1 - cotan^2(x) = -cosech^2(x)$$
The \( arccosech(x) \) is the reciprocal function of the \( cosech(x) \) function, it is defined as follows:
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , \enspace f(x) = arccosech(x) = cosech^{-1}(x) $$
We can calculate this derivative using the derivative of a reciprocal function:
$$ ( f^{-1} )'= \frac{1}{ (f' \circ f^{-1})} $$
$$ with \ \left \{ \begin{gather*}
f(x) = cosech(x) \\
f'(x) = - cosech^2(x) \ cosh(x) \\
f^{-1}(x) = arccosech(x) \end{gather*} \right \} $$
$$ arccosech(x)' = \frac{1}{-cosech^2(arccosech(x)) \times \hspace{0.2em} cosh(arccosech(x))} $$
Furthermore,
$$ cosh^2(x) -sinh^2(x) = 1$$
$$ cosh^2(x) = 1 + sinh^2(x) $$
$$ | cosh(x) | = \sqrt{1 +sinh^2(x)} $$
Since the \(cosh(x)\) function is always positive when \(x \in \mathbb{R}\), we can keep the positive case:
$$ cosh(x) = \sqrt{1 + sinh^2(x)} $$
So,
$$ arccosech(x)' = -\frac{1}{cosech^2(arccosech(x)) \times \sqrt{1 +sinh^2(arccosech(x))}} $$
But:
$$ cosech(x) = \frac{1}{sinh(x)} \Longleftrightarrow sinh(x) = \frac{1}{cosech(x)} $$
Soit,
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1+ \frac{1}{cosech^2(arccosech(x))}}} $$
And as a result,
$$\forall x \in \Bigl[ \mathbb{R} \hspace{0.1em} \backslash \hspace{0.2em} \left \{ 0 \right \} \Bigr] , $$
$$ arccosech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{1 + \frac{1}{ x^2}}} $$
The \( arcsech(x) \) is the reciprocal function of the \( sech(x) \) function, it is defined as follows:
$$ \forall x \in \hspace{0.04em} ]0, \hspace{0.1em} 1] , \enspace f(x) = arcsech(x) = sech^{-1}(x) $$
By the same reasoning as before with \(arccosech(x)'\) calculation:
$$ \forall x \in \hspace{0.1em} ]0, \hspace{0.1em} 1], $$
$$ arcsech(x)' = - \frac{1}{ x^2} \times \frac{1}{ \sqrt{\frac{1}{ x^2} - 1}} $$
The \( arccotanh(x) \) is the reciprocal function of the \( cotanh(x) \) function, it is defined as follows:
$$ \forall \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[ , \enspace f(x) = arccotanh(x) =cotanh^{-1}(x) $$
By the same reasoning as before with \(arccosech(x)'\) calculation:
$$ \forall x \in \hspace{0.04em} ]-\infty, \hspace{0.1em} -1[ \hspace{0.1em} \cup \hspace{0.1em} ]1, \hspace{0.1em} +\infty[, $$
$$ arccotanh(x)' = \frac{1}{ 1 - x^2} $$





 Go to the top of the page
Go to the top of the page