La longueur d'une courbe sur un intervalle
Soit une fonction \(f\) continue sur un intervalle \(I = \bigl[a, b \bigr]\), et \( n \in \mathbb{N}\) un entier naturel.
La longueur de la courbe de \(f\) sur l'intervalle \(I\) vaut :
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$
\text{avec } \left \{ \begin{gather*}
a = x_0 \\
b = x_{n} \\ \\
\Delta_{x} = \frac{b - a}{n} \hspace{2em} (= cte)
\end{gather*} \right \}
$$
Par ailleurs, on peut aussi exprimer cette longueur sous la forme d'une intégrale de Riemann :
$$ L_{\bigl[a, b \bigr]}(f) \approx \int_a^b \sqrt{1 + \bigl[f'(t)\bigr]^2} \ dt $$
Démonstration
Soit une fonction \(f\) continue sur un intervalle \(I = \bigl[a, b \bigr]\), et \( n \in \mathbb{N}\) un entier naturel.
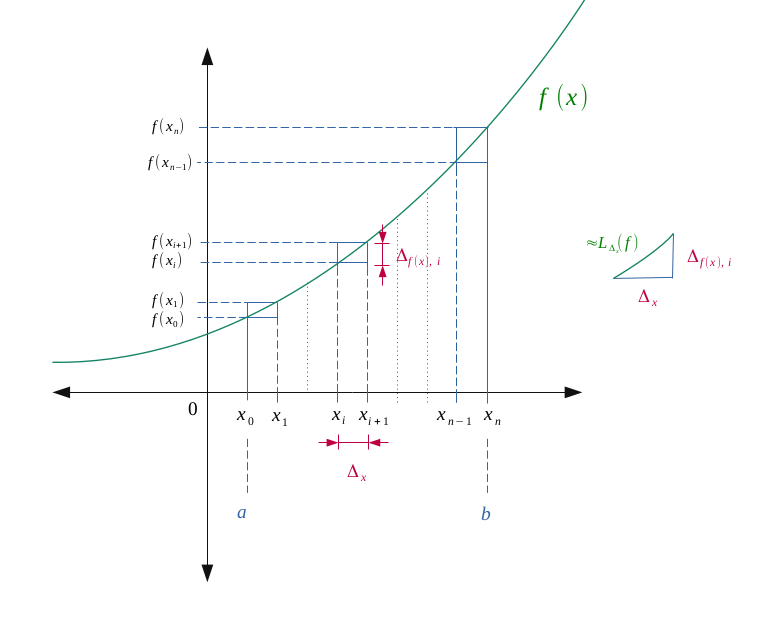
Sur cet intervalle \(I\), subdivisons cet intervalle en une série de points \(\bigl \{x_0, \ x_1, \ ...,\ x_i, \ x_{i+1}, \ ..., \ x_{n - 1}, \ x_{n} \bigr \} \) théoriquement assez petits, et telle que la figure suivante :

On posera alors \(\Delta_{x, \ i}\) tel que :
$$ \forall i \in [\![0, n ]\!], \enspace \Delta_{x, \ i} = x_{i+1}- x_{i} $$
Mais comme \(\Delta_{x, \ i}\) est une constante, elle ne dépend plus de \(i\), on pourra alors la noter \(\Delta_{x}\) :
$$ \forall n \in \mathbb{N}, \enspace \Delta_{x} = \frac{x_{n}- x_{0}}{n} \hspace{2em} (= cte) $$
Il paraît ainsi naturel de remarquer que sur un segment donné \(\Delta_{x} \), la longueur approximative de la courbe \(L_{\Delta_{x}}(f) \) est trouvable en appliquant le théorème de Pythagore :
$$ \forall i \in [\![0, n ]\!], $$
$$ \bigl[L_{\Delta_{x}}(f)\bigr]^2 \approx \bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2 $$
$$ \Bigl( \text{où } \Delta_{f(x), \ i} = f(x_{i+1}) - f(x_{i}) \Bigr) $$
$$ L_{\Delta_{x}}(f) \approx \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \left[\textcolor{#AF5F5F}{\frac{\Delta_{x}}{\Delta_{x}}}\Delta_{f(x), \ i}\right]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \left[\Delta_{x} \frac{\Delta_{f(x), \ i}}{\Delta_{x}}\right]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{x}\bigr]^2 \left[\frac{\Delta_{f(x), \ i}}{\Delta_{x}}\right]^2} \qquad (1) $$
En passant maintenant à la limite quand \(n \to \infty\) pour plus de précision, l'expression \((2)\) fait apparaître la dérivée de \(f\) :
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{x}\bigr]^2 \bigl[f'(x_i)\bigr]^2} \right] \qquad (2) $$
La dérivée de \(f\) qui apparaît est \(f'(x_i)\) car quand \(n \to \infty\), alors \(\ x_{i + 1} \to x_{i} \) :
Enfin, on factorise l'expression :
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 \Bigl( 1 + \bigl[f'(x_i)\bigr]^2\Bigr)} \right] $$
Et comme \(\Delta_{x}\) est une constante, on va pouvoir la sortir en deux temps :
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \Delta_{x} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
Maintenant, s'il on utilise l'intervalle \(I\) entre les points \(a\) et \(b\), pour avoir l'intégralité de la longueur on doit sommer tous ces intervalles.
Nous obtenons alors le résultat suivant:
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$
\text{avec } \left \{ \begin{gather*}
a = x_0 \\
b = x_{n} \\ \\
\Delta_{x} = \frac{b - a}{n} \hspace{2em} (= cte)
\end{gather*} \right \}
$$
Par ailleurs, cela fait beaucoup penser à une intégrale de Riemann.
En effet, si on développe l'expression précédente, on a :
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \left(\frac{b - a}{n}\right) \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \left[f' \left( a + i \times \left(\frac{b - a}{n}\right) \right)\right]^2} \right] $$
Car dans notre cas :
$$ \forall i \in [\![0, n ]\!], \enspace x_i = a + i \times \left(\frac{b - a}{n}\right) $$
Alors, on sait que cette limite tend vers l'intégrale de \(a\) vers \(b\), et par conséquent :
$$ L_{\bigl[a, b \bigr]}(f) \approx \int_a^b \sqrt{1 + \bigl[f'(t)\bigr]^2} \ dt $$






 Retour en haut de page
Retour en haut de page