The length of a curve over an interval
Let be \(f\) a continuous function over an interval \(I = \bigl[a, b \bigr]\), and \( n \in \mathbb{N}\) be a natural number.
The length of the curve of \(f\) over this interval \(I\) is worth:
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$
\text{with } \left \{ \begin{gather*}
a = x_0 \\
b = x_{n} \\ \\
\Delta_{x} = \frac{b - a}{n} \hspace{2em} (= cst)
\end{gather*} \right \}
$$
Moreover, we can express this length as a Riemann integral:
$$ L_{\bigl[a, b \bigr]}(f) \approx \int_a^b \sqrt{1 + \bigl[f'(t)\bigr]^2} \ dt $$
Demonstration
Let be \(f\) a continuous function over an interval \(I = \bigl[a, b \bigr]\), and \( n \in \mathbb{N}\) be a natural number.
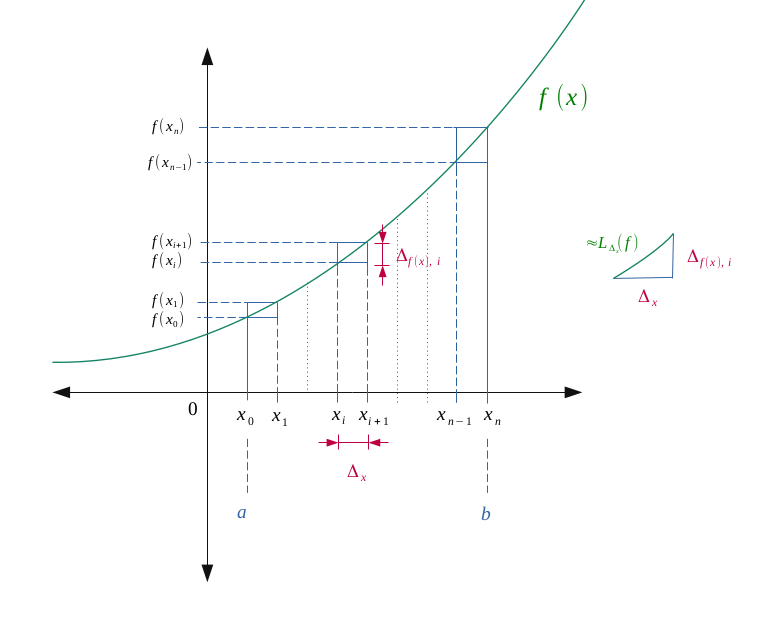
Over this interval \(I\), let us subdivide this interval into a series of points \(\bigl \{x_0, \ x_1, \ ...,\ x_i, \ x_{i+1}, \ ..., \ x_{n - 1}, \ x_{n} \bigr \} \) theoretically quite small, and such as the following figure:

We will then write \(\Delta_{x, \ i}\) and \(\Delta_{f(x), \ i}\) such as:
$$ \forall i \in [\![0, n ]\!], \enspace \Delta_{x, \ i} = x_{i+1}- x_{i} $$
But since \(\Delta_{x, \ i}\) is a constant, it does not depend on \(i\) anymore, we will hence note it \(\Delta_{x}\):
$$ \forall n \in \mathbb{N}, \enspace \Delta_{x} = \frac{x_{n}- x_{0}}{n} \hspace{2em} (= cte) $$
It therefore seems natural to note that on a given segment \(\Delta_{x} \), the approximate length of the curve \(L_{\Delta_{x}}(f) \) can be found by applying the Pythagorean theorem:
$$ \forall i \in [\![0, n ]\!], $$
$$ \bigl[L_{\Delta_{x}}(f)\bigr]^2 \approx \bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2 $$
$$ \Bigl( \text{where } \Delta_{f(x), \ i} = f(x_{i+1}) - f(x_{i}) \Bigr) $$
$$ L_{\Delta_{x}}(f) \approx \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{f(x), \ i}\bigr]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \left[\textcolor{#AF5F5F}{\frac{\Delta_{x}}{\Delta_{x}}}\Delta_{f(x), \ i}\right]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \left[\Delta_{x} \frac{\Delta_{f(x), \ i}}{\Delta_{x}}\right]^2} $$
$$ L_{\Delta_{x}}(f) \approx \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{x}\bigr]^2 \left[\frac{\Delta_{f(x), \ i}}{\Delta_{x}}\right]^2} \qquad (1) $$
Now, taking the limit when \(n \to \infty\) for much precision, the expression \((2)\) reveals the derivative of \(f\):
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 + \bigl[\Delta_{x}\bigr]^2 \bigl[f'(x_i)\bigr]^2} \right] \qquad (2) $$
The derivative of \(f\) which appears as \(f'(x_i)\) because when \(n \to \infty\), then \(\ x_{i + 1} \to x_{i} \):
Finally, we factorize the expression:
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \sqrt{\bigl[\Delta_{x}\bigr]^2 \Bigl( 1 + \bigl[f'(x_i)\bigr]^2\Bigr)} \right] $$
And since \(\Delta_{x}\) we will be able to extract it in two steps:
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \left[ \sum_{i = 0}^{n - 1} \Delta_{x} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$ L_{\Delta_{x}}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
Now, if we use the interval \(I\) between the two points \(a\) and \(b\), to get the total length, we must sum all these intervals.
And as a result, we do have that:
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \Delta_{x} \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \bigl[f'(x_i)\bigr]^2} \right] $$
$$
\text{avec } \left \{ \begin{gather*}
a = x_0 \\
b = x_{n} \\ \\
\Delta_{x} = \frac{b - a}{n} \hspace{2em} (= cst)
\end{gather*} \right \}
$$
Moreover, the preivous formula make us think of a Riemann integral.
Indeed, if we expand the previous expression, we do obtain this:
$$ L_{\bigl[a, b \bigr]}(f) \approx \lim_{n \to \infty} \left(\frac{b - a}{n}\right) \left[ \sum_{i = 0}^{n - 1} \sqrt{1 + \left[f' \left( a + i \times \left(\frac{b - a}{n}\right) \right)\right]^2} \right] $$
Because in our case:
$$ \forall i \in [\![0, n ]\!], \enspace x_i = a + i \times \left(\frac{b - a}{n}\right) $$
Alors, on sait que cette limite tend vers the integral from \(a\) towards \(b\), and therefore:
$$ L_{\bigl[a, b \bigr]}(f) \approx \int_a^b \sqrt{1 + \bigl[f'(t)\bigr]^2} \ dt $$






 Go to the top of the page
Go to the top of the page