Convergence criteria for series

Series with positive terms

In this part, only the case of series with positive terms , but the same principle then also applies to series with negative terms, because if we consider two series:

a series with positive terms: $S_+$
a series with negative terms: $S_-$

Both vary by only one sign $(-)$ in factor:

$$ S_+ = - S_+ $$

Fundamental criteria of convergence

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence.

$$ \sum u_n \text{ converges } \Longrightarrow \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

So, if a sequence has a non-zero limit, we directly deduce that it is divergent.

Comparison with a reference series

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence whose nature wish to know.

We can compare this sequence term by term with another sequence $(U_n)_{n \in \mathbb{N}}$ whose nature is known.

$$ \Bigl[ s_n \leqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = M \Bigr] \Longrightarrow s_n \text{ converges and } (s_n < M) $$

$$ \text{with : } \left \{ s_n = \sum_{k = 0}^n u_n, \hspace{2em} S_n = \sum_{k = 0}^n U_n \right \} $$

Symmetrically, we have the complement:

$$ \Bigl[ s_n \geqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = + \infty \Bigr] \Longrightarrow s_n \text{ diverges} $$

D'Alembert's rule

If in a series with positive terms $\sum u_n$, we always have, from a certain rank:

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverges} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{we can't make any affirmation} $$

$$ \text{(D'Alembert's rule)}$$

Cauchy's rule

If in a series with positive terms $\sum u_n$, we always have, from a certain rank:

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverges} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{we can't make any affirmation} $$

$$ \text{(Cauchy's rule)}$$

Rule of $n^{\alpha} u_n$

Let there be two series with positive terms $\Bigl(\sum u_n, \sum v_n \Bigr)$.

If we can find any $\alpha \in \mathbb{R}^*_+$ such as:

$$ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

Alors,

$$ \alpha > 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \alpha \leqslant 1 \Longrightarrow \sum u_n \text{ diverges} $$

$$ \text{(Rule of $n^{\alpha} u_n$)}$$

Integrals-series comparison

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence with positive terms and $f(n)$ its associated decreasing piecewise continuous function.

We can bound a series by integrals to approximate it such as:

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

$$ (\text{with } u_n = f(n)) $$

Alternating series

Specific criteria for alternating series

For any decreasing sequence with positive terms $(u_n)_{n \in \mathbb{N}}$ and its alternating series $(A_n)$:

$$ \left[ \lim_{n \to \infty} u_n = 0 \right] \Longrightarrow A_n \text{ converges and } (A_n < u_1) $$

$$ \left(\text{with } A_n = \sum_{k \geqslant 1} \Bigl[ (-1)^{k + 1} \ u_k \Bigr]\right) $$

Demonstrations

Series with positive terms

Fundamental criteria of convergence

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence and $(S_n)$ its partial series, such as:

$$ S_n = \sum_{k = 0}^n u_n $$

The convergence of such a series implies that there exists a certain natural number $p$ such as:

$$ \lim_{n \to + \infty} \bigl[ S_{n + p} - S_n \bigr] = 0 \qquad (1) $$

Which is to say that, if we make the difference $ (S_{n + p} - S_n) $:

$$ S_{n + p} - S_n = u_{n + 1} + u_{n + 2} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} $$

$$ with \enspace \left \{ \begin{gather*} S_n = u_0 + u_1 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n - 1} + u_n \\ \\ S_{n + p} = u_0 + u_1 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n - 1} + u_n \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} \end{gather*} \right \} $$

So, by rewriting $(1)$ under its new form:

$$ \lim_{n \to + \infty} \bigl[ u_{n + 1} + u_{n + 2} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{n + p - 1} + u_{n + p} \bigr] = 0 \qquad (1') $$

Since this condition is true for any value of $p$, with $(p = 1)$, we do have:

$$ \lim_{n \to + \infty} \bigl[ u_{n + 1} \bigr] = 0 $$

Which is the same as writing:

$$ \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

We therefore obtain as a result the necessary condition, to prove that a series converges, that its associated sequence has zero limit.

$$ \sum u_n \text{ converges } \Longrightarrow \lim_{n \to + \infty} \bigl[ u_n \bigr] = 0 $$

So, if a sequence has a non-zero limit, we directly deduce that it is divergent.

Comparison with a reference series

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence whose nature wish to know.

We can compare this sequence term by term with another sequence $(U_n)_{n \in \mathbb{N}}$ whose nature is known.

Let us then assume that all the terms of the sequence $(u_n)$ are less than or equal to those of the sequence $(U_n)$, such as:

$$ u_0 + u_1 + u_2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_n \leqslant U_0 + U_1 + U_2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} U_n $$

Let us put that:

$$ s_n = \sum_{k = 0}^n u_n $$

$$ S_n = \sum_{k = 0}^n U_n $$

From the above, we have:

$$ s_n \leqslant S_n $$

Let us suppose as well that $(U_n)$ is known:

$$ \exists M \in \mathbb{R}, \ \lim_{n \to +\infty} S_n = M $$

Therefore, we will always have that:

$$ s_n \leqslant S_n < M $$

So the series $(s_n)$ is also strictly majorized by $M$.

Since it is a series resulting from a sequence with positive terms, it is increasing. Being increasing and bounded above, it necessarily converges.

$$ \Bigl[ s_n \leqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = M \Bigr] \Longrightarrow s_n \text{ converges and } (s_n < M) $$

$$ \text{with : } \left \{ s_n = \sum_{k = 0}^n u_n, \hspace{2em} S_n = \sum_{k = 0}^n U_n \right \} $$

Symmetrically, we have the complement:

$$ \Bigl[ s_n \geqslant S_n \Bigr] \land \Bigl[ \lim_{n \to +\infty} S_n = + \infty \Bigr] \Longrightarrow s_n \text{ diverges} $$

D'Alembert's rule

Let $(u_n)_{n \in \mathbb{N}}$ be numerical sequence with positive terms.

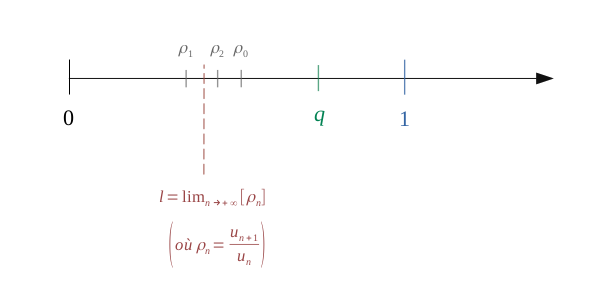
Let us assume that the ratio $\left(\rho_n = \frac{u_{n + 1}}{u_n}\right)$ tends towards a certain limit $l$ (finite or extremity):

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = l $$

if $(l < 1)$

If $(l < 1)$, then we can choose a natural number $(m \leqslant n)$ sufficiently large, from which the next terms of the sequence will possibly oscillate around a certain value, but will in any case converge towards the latter. We can then find a new ratio $q$ which will always be superior to it.

In this case,

$$ \frac{u_{m + 1}}{u_m} < q < 1 \qquad (H) $$

This hypothesis implies that:

$$ u_{m + 1} < u_m \ q $$

So, we can establish a comparison between an index and the following:

$$ u_{m + 1} < u_m \ q $$

By multiplying by $q$ on each side:

$$ u_{m + 1} \ q < u_m \ q^2 \qquad (2) $$

$$ u_{m + 2} < u_{m + 1} \ q \qquad (2') $$

With both expressions $(2)$ and $(2')$, we obtain that:

$$ u_{m + 2} < u_{m + 1} \ q < u_m \ q^2 $$

Then we can repeat the operation indefinitely until we obtain:

$$ u_{m + p} < u_m \ q^p $$

In this way, each following term $u_m$ is less than that of a geometric progression of reason $q$:

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... < u_m + u_m \ q + u_m \ q^2 \hspace{0.2em} ... $$

But, by our hypothesis $(H)$, we do have $(q < 1)$. So the geometric series of reason $q$ converge, and the same is true for a series which is inferior to it term by term. Thus,

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converges} $$

if $(l > 1)$

Following the same reasoning as for the previous case, we see that:

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... > u_m + u_m \ q + u_m \ q^2 \hspace{0.2em} ... $$

But here $(q > 1)$, so the geometric series diverges, and it is the same for the series $\sum u_n$ which is superior to it term by term..

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverges} $$

if $(l = 1)$

In the latter case, nothing can be said in general.

Indeed, consider the following series:

$$ \sum_{k = 1}^n \frac{1}{k^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \frac{1}{n^p} \qquad (\text{with } p \in \mathbb{N}^*) $$

The ratio $\frac{u_{n + 1}}{u_n} $ to consider is that of the general term of its associated sequence: $u_n = \frac{1}{n^p} $, so:

$$ \frac{u_{n + 1}}{u_ n} = \frac{\frac{1}{(n + 1)^p}}{\frac{1}{n^p}} $$

$$ \frac{u_{n + 1}}{u_ n} = \frac{n^p}{(n + 1)^p} $$

$$ \frac{u_{n + 1}}{u_ n} = \left(\frac{n}{n + 1} \right)^p $$

Which can be arranged in:

$$ \frac{u_{n + 1}}{u_ n} = \left(\frac{n \textcolor{#606B9E}{+ 1 - 1}}{n + 1} \right)^p = \left(1 - \frac{1}{n + 1} \right)^p $$

Regardless of $p$, its limits is worth:

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1^- $$

But we know that the series of the type $ \underset{k \leqslant 1}{\sum} \frac{1}{k^p}$ are Riemann series and:

if $(\alpha = 1) $: the series is divergent (harmonic series)
if $(\alpha > 1) $: the series is convergent

This counterexample clearly shows that there is no general law to conclude on the nature of the series, knowing only with the result of the limit of the ratio $\frac{u_{n + 1}}{u_n}$.

So,

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{we can't make any affirmation} $$

And as result,

If in a series with positive terms $\sum u_n$, we always have, from a certain rank:

$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] < 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] > 1 \Longrightarrow \sum u_n \text{ diverges} $$
$$ \lim_{n \to + \infty} \left[ \frac{u_{n + 1}}{u_n} \right] = 1 \Longrightarrow \text{we can't make any affirmation} $$

$$ \text{(D'Alembert's rule)}$$

Cauchy's rule

Let $(u_n)_{n \in \mathbb{N}}$ be numerical sequence with positive terms.

This rule is very similar to D'Alembert's rule, but here we will study the result of the limit of the $n$-th root of the general term of the sequence $(u_n)$.

$$ \lim_{n \to \infty} \sqrt[n]{u_n} = l $$

if $(l < 1)$

Si $(l < 1)$, then we can choose a natural number $(m \leqslant n)$ ssufficiently large, from which the next terms of the sequence will possibly oscillate around a certain value, but will in any case converge towards the latter. We can then find a new root $q$ which will always be superior to it.

In this case,

$$ \sqrt[m]{u_m} < q < 1 \qquad (H^*) $$

So, we can establish a comparison between an index and the following:

$$ \sqrt[m]{u_m} < q $$

$$ \sqrt[{m + 1}]{u_{m + 1}} < q $$

Taking the power of each member, we have:

$$ \left( \sqrt[m]{u_m} \right)^m < q^m $$

$$ u_m < q^m $$

$$ \left( \sqrt[m + 1]{u_{m + 1}} \right)^{m + 1} < q^{m + 1} $$

$$ u_{m + 1} < q^{m + 1} $$

The terms of the series $\sum u_n$ are therefore all lower than those of a geometric series of reason $q$ :

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... < q^n + q^{m + 1} + q^{m + 2} \hspace{0.2em} ... $$

But, this series converge because $(q < 1)$, so it is the same thing for $\sum u_n$ which is inferior to it term by term.

So,

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converges} $$

if $(l > 1)$

Following the same reasoning as for the previous case, we see that:

$$ u_m + u_{m + 1} + u_{m + 2} \hspace{0.2em} ... > q^n + q^{m + 1} + q^{m + 2} \hspace{0.2em} ... $$

But here $(q > 1)$, so the geometric series diverges, and it is the same for the series $\sum u_n$ which is superior to it term by term.

$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverges} $$

if $(l = 1)$

In the latter case, nothing can be said in general.

ndeed, if we consider the same series as for the previous example:

$$ \sum_{k = 1}^n \frac{1}{k^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \frac{1}{n^p} \qquad (\text{with } q \in \mathbb{N}^*) $$

The root to consider $\sqrt[n]{u_n}$ is that of the general term of its associated sequence: $u_n = \frac{1}{n^p} $, so:

$$ \sqrt[n]{u_n} = \sqrt[n]{\frac{1}{n^p}} $$

$$ \sqrt[n]{u_n} = \left(\frac{1}{n^p}\right)^{\frac{1}{n}} $$

$$ \sqrt[n]{u_n} = \frac{1}{n^{\frac{p}{n}}} $$

Regardless of $p$, its limit is worth:

$$ \lim_{n \to + \infty} \sqrt[n]{u_n} = 1 $$

But we know that the series of the type $ \underset{k \leqslant 1}{\sum} \frac{1}{k^p}$ are Riemann series and:

if $(\alpha = 1) $: the series is divergent (harmonic series)
if $(\alpha > 1) $: the series is convergent

This counterexample clearly shows that there is no general law to conclude on the nature of the series, knowing only with the result of the limit of the root $\sqrt[n]{u_n}$.

So,

$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{we can't make any affirmation} $$

And as a result,

If in a series with positive terms $\sum u_n$, we always have, from a certain rank:

$$ \lim_{n \to \infty} \sqrt[n]{u_n} < 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} > 1 \Longrightarrow \sum u_n \text{ diverges} $$
$$ \lim_{n \to \infty} \sqrt[n]{u_n} = 1 \Longrightarrow \text{we can't make any affirmation} $$

$$ \text{(Cauchy's rule)}$$

Rule of $n^{\alpha} u_n$

Let $\alpha \in \mathbb{R}^*_+$ a strictly positive number and $(v_n)_{n \in \mathbb{N}}$ a numerical sequence having positive terms:

$$ \forall n \in \mathbb{N}^*, \ v_n = \frac{1}{n^{\alpha}} $$

If we study the ratio $\frac{u_n}{v_n}$, we obtain:

$$ \frac{u_n}{v_n} = \frac{u_n}{\frac{1}{n^{\alpha}}} $$

$$ \frac{u_n}{v_n} = n^{\alpha} u_n $$

Now, we know from the following property that for two sequences with terms of constant sign $(c_n, d_n)_{n \in \mathbb{N}}$:

$$ \lim_{n \to + \infty} \left[ \frac{c_n}{d_n} \right] = l > 0 \Longrightarrow \text{$\sum c_n$ and $\sum d_n$ have the same nature} $$

But we know that the series of type $\sum v_n$ are Riemann series and:

if $(\alpha > 1)$

If $(\alpha > 1)$, then the series $ \underset{k \leqslant 1}{\sum} \frac{1}{k^{\alpha}}$ is convergent.

Then, if we can proove that:

$$ \exists \alpha > 1, \ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

We will obtain as a result that the series $\sum u_n$ also converge.

if $(\alpha \leqslant 1)$

Now $(\alpha \leqslant 1)$, then the series $ \underset{k \leqslant 1}{\sum} \frac{1}{k^{\alpha}}$ is divergent, and if we prove that:

$$ \exists \alpha \leqslant 1, \ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

We will obtain as a result that the series $\sum u_n$ also diverge.

Si l'on peut trouver $\alpha \in \mathbb{R}^*_+$ tel que :

$$ \lim_{n \to + \infty} (n^{\alpha} u_n) = l > 0 $$

Alors,

$$ \alpha > 1 \Longrightarrow \sum u_n \text{ converges} $$
$$ \alpha \leqslant 1 \Longrightarrow \sum u_n \text{ diverges} $$

$$ \text{(Rule of $n^{\alpha} u_n$)}$$

Integrals-series comparison

Let $(u_n)_{n \in \mathbb{N}}$ be a numerical sequence with positive terms and $f(n)$ its associated decreasing piecewise continuous function.

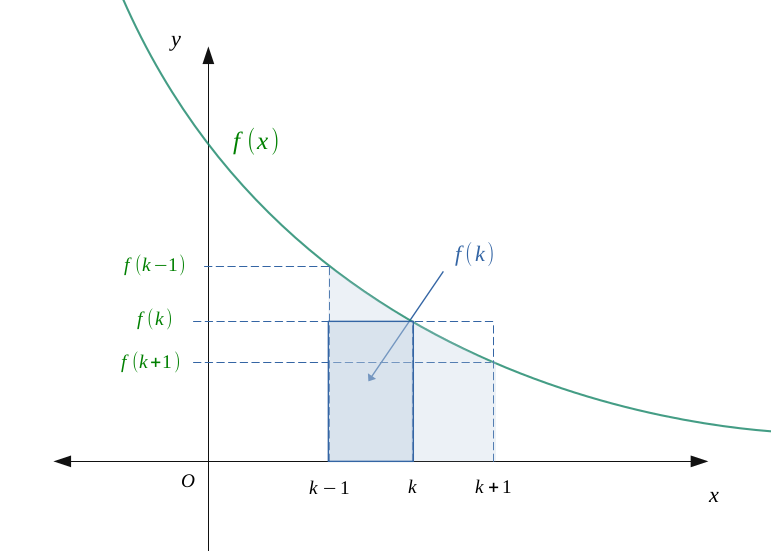
We had represented an example of it on the following figure:

The highlighted rectangle is worth $f(k)$. We can then bound the series $\sum u_n$ by two integrals:

$$ \int_{k}^{k + 1} f(t) \ dt \leqslant f(k) \leqslant \int_{k - 1}^k f(t) \ dt $$

By performing the sum from $(k = 1)$ unitl $n$, we do obtain that:

$$ \sum_{k = 0}^n \left(\int_{k}^{k + 1} f(t) \ dt \right)\leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \left(\int_{k - 1}^k f(t) \ dt \right) $$

$$ \int_{1}^{2} f(t) \ dt + \int_{2}^{3} f(t) \ dt \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \int_{n - 1}^{n} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \int_{0}^{1} f(t) \ dt + \int_{1}^{2} f(t) \ dt \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \int_{n}^{n + 1} f(t) \ dt $$

We can know use the Chasles relation to gather terms:

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

Thus, we can bound a series by integrals to approximate it such as:

$$ \int_{1}^{n + 1} f(t) \ dt \leqslant \sum_{k = 0}^n f(k) \leqslant \sum_{k = 0}^n \int_{0}^n f(t) \ dt $$

$$ (\text{with } u_n = f(n)) $$

Alternating series

Specific criteria for alternating series

Let $(u_n)_{n \in \mathbb{N}^*}$ a decreasing sequence with positive terms:

$$ \lim_{n \to \infty} u_n = 0 $$

As well, let $A_n$ be its associated series, alternatively positive and negative:

$$ A_n = \sum_{k = 1}^n \Bigl[ (-1)^{k + 1} \ u_k \Bigr] = u_1 - u_2 + u_3 - u_4 \hspace{0.2em} ... $$

Well, the sum of the $2n$ terms can be written as:

$$ A_{2n} = u_1 - u_2 + u_3 - u_4 \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} u_{2n - 1} - u _{2n} $$

We can gather terms in this way:

$$ A_{2n} = \underbrace{(u_1 - u_2)} _{\geqslant 0} + \underbrace{(u_3 - u_4)} _{\geqslant 0} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} \underbrace{(u_{2n - 1} - u _{2n})} _{\geqslant 0} \qquad(3) $$

As the sequence is decreasing by hypothesis, the gathered terms are all positive. The series $(A_n)$ is therefore increasing.

In addition, by now displaying $(A_n)$ under the form $(3')$, we notice that $(A_{2n})$ is always lower than $u_1$:

$$ A_{2n} = u_1 - \underbrace{(u_2 - u_3)} _{\geqslant 0} - \underbrace{(u_4 - u_5)} _{\geqslant 0} \hspace{0.2em} - \hspace{0.2em} ... \hspace{0.2em} - \hspace{0.2em} \underbrace{u_{2n}} _{\geqslant 0} \qquad(3') $$

As a consequence of it, $(A_n)$ being increasing and majozrized by $u_1$, it is convergent and its value never exceed this latter.

So, for any decreasing sequence $(u_n)_{n \in \mathbb{N}}$ ad its associated alternating series $(A_n)$:

$$ \left[ \lim_{n \to \infty} u_n = 0 \right] \Longrightarrow A_n \text{ converges and } (A_n < u_1) $$

$$ \left(\text{with } A_n = \sum_{k \geqslant 1} \Bigl[ (-1)^{k + 1} \ u_k \Bigr]\right) $$

Examples

Example of a series-integrals comparison

We try to study the convergence of the following series :

$$ S_n = \sum_{k = 1}^n \frac{1}{k^2} $$

Since the corresponding function:

$$ f(n) = \frac{1}{n^2} $$

is definitely positive and decreasing, the we can use the series-integrals comparison method:

$$ \int_{k}^{k + 1} \frac{dt}{t^2} \leqslant f(k) \leqslant \int_{k - 1}^k \frac{dt}{t^2} \ dt $$

We perform the sum of each elements from $(k = 2)$ until $n$ (because we will see below that $\displaystyle \int^x f(t) \ dt$ is not defined at $0$):

$$ \int_{2}^{n + 1} \frac{dt}{t^2} \leqslant \sum_{k = 2}^n f(k) \leqslant \int_{1}^n \frac{dt}{t^2} \ dt $$

Let us now find a primitive of $f$. It is standard derivative:

$$ \int^x \frac{dt}{t^2} = -\frac{1}{t}$$

So by replacing:

$$ \left[ -\frac{1}{t} \right]_2^{n + 1} \leqslant \sum_{k = 2}^n f(k) \leqslant \left[ -\frac{1}{t} \right]_1^{n} $$

We manually add $f(1)$ to obtain the full sum:

$$ f(1) + \left[ -\frac{1}{t} \right]_2^{n + 1} \leqslant \sum_{k = 1}^n f(k) \leqslant f(1) + \left[ -\frac{1}{t} \right]_1^{n} $$

$$ 1 -\frac{1}{n + 1} + \frac{1}{2} \leqslant \sum_{k = 1}^n f(k) \leqslant 1 -\frac{1}{n} + 1 $$

$$ \frac{3}{2} -\frac{1}{n + 1} \leqslant S_n \leqslant 2 -\frac{1}{n} $$

And we can now make tend everything towards the infinite.

$$ \lim_{n \to +\infty} \left[ \frac{3}{2} -\frac{1}{n + 1} \right] \leqslant \lim_{n \to +\infty} \bigl[ S_n \bigr] \leqslant \lim_{n \to +\infty} \left[ 2 -\frac{1}{n} \right] $$

$$ \frac{3}{2} \leqslant \lim_{n \to +\infty} \bigl[ S_n \bigr] \leqslant 2 $$

This series is definitely convergent because it is bounded.

Go to the top of the page

Convergence criteria for series

Demonstrations

Examples

Example of a series-integrals comparison