Analytical geometry in space

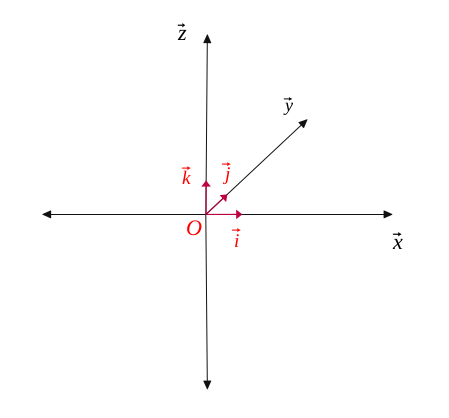
Let be $(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})$ an orthonormal coordinate system in space.

Parametric equation of a straight line in space

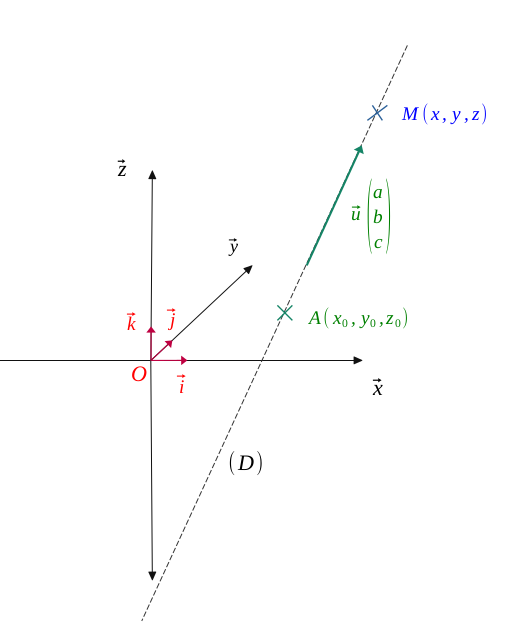
The parametric equation of a straight line $\mathcal{D}$ in space, passing through a point $A(x_0, y_0, z_0)$ and directed by a vector $\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix} $ (with $a, b, c $ all three non-zero) is:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

$$ M\bigl[x, y, z \bigr] \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x = at + x_0 \\ y = bt + y_0 \\z = ct + z_0 \end{Bmatrix} $$

$$ with \enspace \Biggl \{ \begin{gather*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ three \ real\ numbers\ which \ are \ non-zero \ simultaneously \end{gather*} $$

Equation of a plane

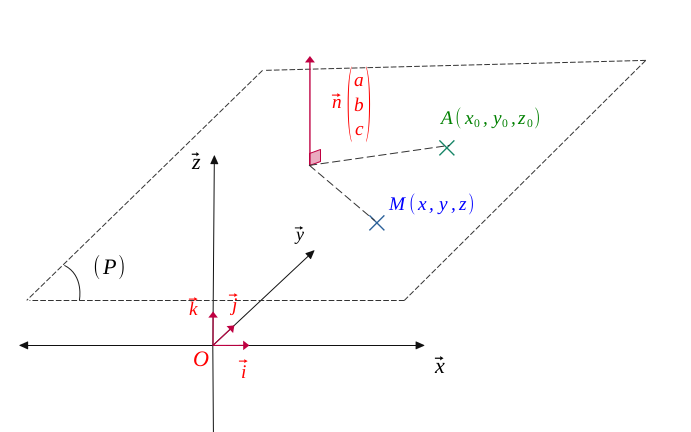
The equation of a place $(\mathcal{P})$ in space, passing through a point $A(x_0, y_0, z_0)$ and orthogonal to a vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$ (with $a, b, c $ all three non-zero) is:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

$$ M\bigl[x, y, z \bigr] \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} ax + by + cz + d = 0$$

$$ with \enspace \Biggl \{ \begin{gather*} (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ three \ real\ numbers\ which \ are \ non-zero \ simultaneously \\ d = -ax_0 - by_0 -c z_0 \end{gather*} $$

Distance from a point to a plane

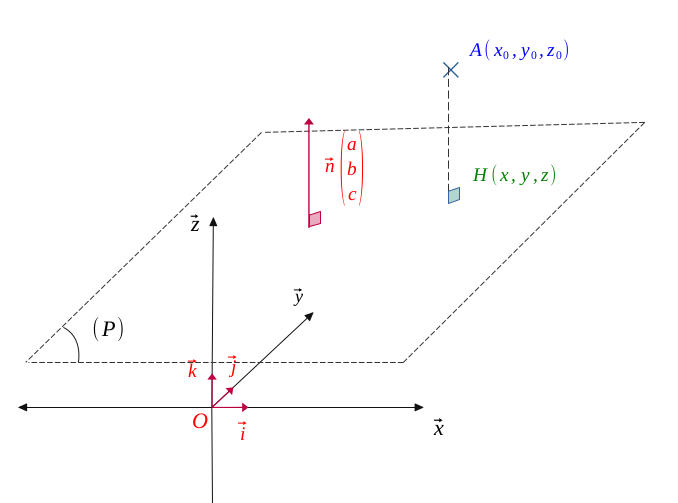
Let $\mathcal{P}$ be a plane orthogonal to a vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$ (with $a, b, c $ all three non-zero), having as equation:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, \ ax + by + cz + d = 0$$

The distance from a point $A(x_0, y_0, z_0)$ in relation to this plane $(\mathcal{P})$ orthogonally projecting on this plane at point $H(x, y, z)$ is worth:

$$ d(A, \mathcal{P}) = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$

Projection of a sum of vectors upon a plane

The projection of a sum of vectors is the sum of each vector's projection

Projection of the sum of two vectors, sum of the two respective projections

$$ \forall n \in \mathbb{N}, \ \forall (\vec{u_1}, \vec{u_2}, \ ..., \vec{u_n}), $$

$$ proj\left(\sum_{k=0}^n \overrightarrow{ u_k} \right) = \sum_{k=0}^n proj(\overrightarrow{u_k})$$

Geometrical figures

Equation of a sphere

The sphere $(\mathcal{S})$ having a radius $R$ and centered at point $A(x_0, y_0, z_0)$ has for equation in space:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$

$$ (with \enspace (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3) $$

Equation of a cylinder

The cylinder$(\mathcal{C})$ having a radius $r$ and centered at point $A(x_0, y_0, z_0)$ has for equation in space:

$$ \forall (x, y) \in \hspace{0.05em}\mathbb{R}^2, $$

$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} r^2 = (x-x_0)^2 + (y-y_0)^2 $$

$$ (with \enspace (x_0, y_0) \in \hspace{0.05em} \mathbb{R}^2) $$

Equation of a cone

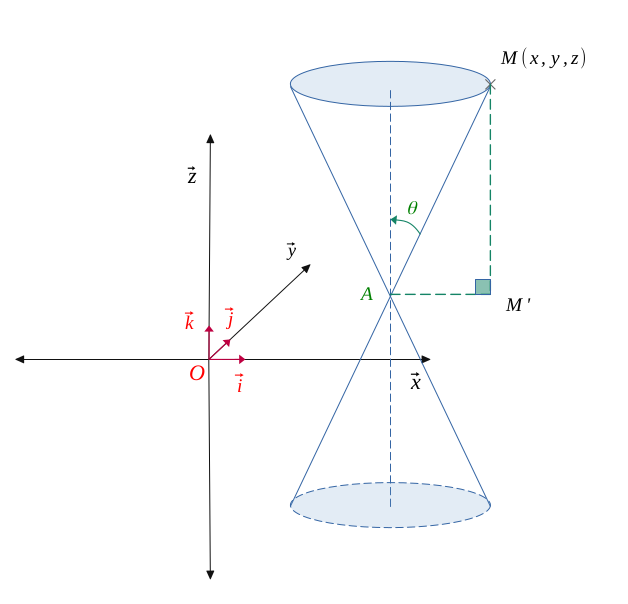
The cone $(\mathcal{C})$ having a half-angle $ \theta$, and centered at point $A(x_0, y_0, z_0)$ has for equation in space:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} (x- x_0)^2 + (y- y_0)^2 = k(z-z_0)^2 $$

$$ with \enspace \Biggl \{ \begin{gather*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ k = tan^2(\theta) \end{gather*} $$

Coordinates system

From cartesian to spherical coordinates

Longitude-latitude coordinates

Spherical coordinates: longitude-latitude

$$ \Biggl \{ \begin{gather*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \\ z = R \ sin(\varphi) \end{gather*} \qquad (\theta : longitude- \varphi : latitude) $$

$$with \enspace \left \{ \begin{gather*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{gather*} \right \}$$

Longitude-colatitude coordinates

Spherical coordinates: longitude-colatitude

$$ \Biggl \{ \begin{gather*} x = R \ sin(\psi) \ cos(\theta) \\ y = R \ sin(\psi) \ sin(\theta) \\ z = R \ cos(\psi) \end{gather*} \qquad (\theta : longitude- \psi : colatitude) $$

$$with \enspace \left \{ \begin{gather*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \psi = arccos \left( \frac{z}{R} \right) \end{gather*} \right \}$$

Demonstrations

Lines and planes

Parametric equation of a straight line

Let $(\mathcal{D})$ be a straight line in space, passing through a point $A(x_0, y_0, z_0)$ and directed by a vector $\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix} $ (with $(a, b, c) \in \hspace{0.05em} \mathbb{R}^3 $ three real numbers which are non-zero simultaneously).

As $M \in \mathcal{D}$, so the vectors $\vec{u}$ and $\overrightarrow{AM}$ are collinear. Thus:

$$ M\bigl[x, y, z \bigr] \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \overrightarrow{AM} = t \times \overrightarrow{u}$$

$$ \Longleftrightarrow \exists^{\infty} t \in \mathbb{R}, \enspace \begin{pmatrix} x -x_0 \\ y - y_0 \\z - z_0 \end{pmatrix} = \hspace{0.1em} \begin{pmatrix} ta \\ tb \\tc \end{pmatrix} $$

$$ \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x -x_0 = at\\ y - y_0 = bt \\z - z_0 = ct \end{Bmatrix} $$

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

The parameter $t$ is a free parameter that can take any value.

In fact, the line $(\mathcal{D})$ extending to infinity, we obtain a formation of this latter by varying $t$, leading to the intersection of three planes corresponding respectively to the three equations; which forms a series of points in space.

Parametric equation of a straight line in space - superposition of planes forming a line according to t

Equation of a plane

Let $(\mathcal{P})$ be a plane in space, passing through a point $A(x_0, y_0, z_0)$ and orthogonal to a vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$ (with $(a, b, c) \in \hspace{0.05em} \mathbb{R}^3 $ three real numbers which are non-zero simultaneously).

So, any point $M\bigl[x, y, z \bigr]$ belonging to this plane is orthogonal to $\vec{n}$.

$$ M\bigl[x, y, z \bigr] \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \overrightarrow{MA} \perp \vec{n}$$

Two orthogonal vectors have their scalar product worthing zero.

$$ \Longleftrightarrow \hspace{0.1em} \overrightarrow{MA} .\vec{n} = 0$$

$$ \Longleftrightarrow \begin{pmatrix} x -x_0 \\ y - y_0 \\z - z_0 \end{pmatrix} . \hspace{0.1em} \begin{pmatrix} a \\ b \\c \end{pmatrix} = 0$$

$$ a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 $$

$$ ax - ax_0 + by - by_0 + cz -c z_0 = 0 $$

$$ ax + by + cz \hspace{0.1em} \underbrace{-ax_0 - by_0 -c z_0} _\text{$ (d \hspace{0.1em} \in \hspace{0.05em} \mathbb{R})$} \hspace{0.1em} = 0 $$

$$ ax + by + cz + d = 0 $$

The equation of a place $(\mathcal{P})$ in space, passing through a point $A(x_0, y_0, z_0)$ and orthogonal to a vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$ is:

$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$

$$ M\bigl[x, y, z \bigr] \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} ax + by + cz + d = 0$$

$$ with \enspace \Biggl \{ \begin{gather*} (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ three \ real\ numbers\ which \ are \ non-zero \ simultaneously \\ d = -ax_0 - by_0 -c z_0 \end{gather*} $$

Distance from a point to a plane

Let $(\mathcal{P})$ be a plane in space, orthogonal to a vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$(with $(a, b, c) \in \hspace{0.05em} \mathbb{R}^3 $ three real numbers which are non-zero simultaneously).

Let $A(x_0, y_0, z_0)$ be a point orthogonally projecting on $(\mathcal{P})$ at point $H(x, y, z)$.

We are trying to estimate the distance $AH$, shortest distance from the point $A$ to the plane $(\mathcal{P})$.

By the definition of the scalar product, we do have:

$$ \overrightarrow{AH} .\vec{n} = ||\overrightarrow{AH} || \times ||\overrightarrow{n} || \times cos(\overrightarrow{AH}, \overrightarrow{n}) $$

$$ \overrightarrow{AH} .\vec{n} = AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) \qquad (1)$$

On the other hand, with the calculation of the scalar product by the coordinates product, we do have:

$$ \overrightarrow{AH} .\vec{n} = a(x-x_0) + b(y-y_0) + c(z-z_0) $$

$$ \overrightarrow{AH} .\vec{n} = \hspace{0.1em} \underbrace{ax + by + c z} _\text{$ -d $} \ -ax_0 - by_0 -c z_0 $$

$$ \overrightarrow{AH} .\vec{n} = -ax_0 - by_0 -c z_0 -d \qquad (2) $$

Given that $(1)$ and $(2)$ are equal, being the smae scalar product, we now have:

$$ AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) = -ax_0 - by_0 -c z_0 -d $$

Calculant une distance, on peut passer en valeur absolue :

$$ \Bigl | AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) \Bigr | = \Bigl | -ax_0 - by_0 -c z_0 -d \Bigr | $$

$$AH = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\Bigl |\sqrt{a^2 + b^2 + c^2} \times (\pm 1) \Bigr |} $$

$$AH = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$

The distance from a point $A(x_0, y_0, z_0)$ in relation to this plane $(\mathcal{P})$ orthogonally projecting on this plane at point $H(x, y, z)$ is worth:

$$ d(A, \mathcal{P}) = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$

Projection of a sum of vectors upon a plane

In this part, the term projection will always means orhtogonal projection.

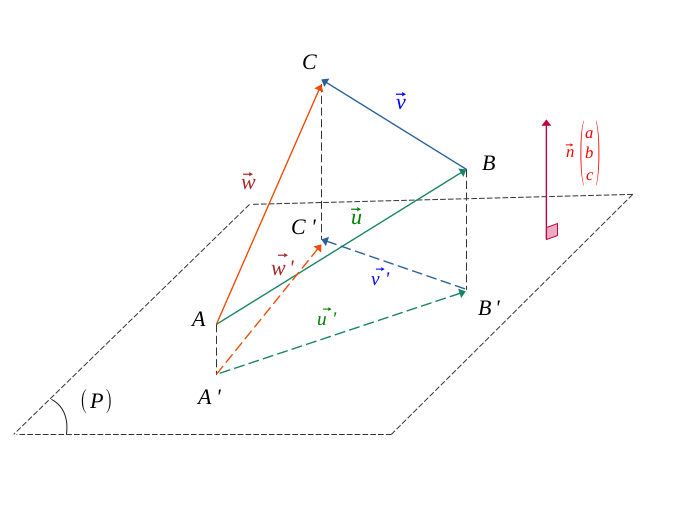
Let $(\mathcal{P})$ be a plane having as normal vector $\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}$, and two non-null vectors being non-collinear to this plane, $\vec{u}\begin{pmatrix} x_1\\ y_1 \\z_1 \end{pmatrix}$ and $\vec{v}\begin{pmatrix} x_2\\ y_2 \\z_2\end{pmatrix}$.

Let us call $\vec{u'}$ and $\vec{v'}$ the respective projections of the two vectors $\vec{u}$ and $\vec{v}$ upon this plane.

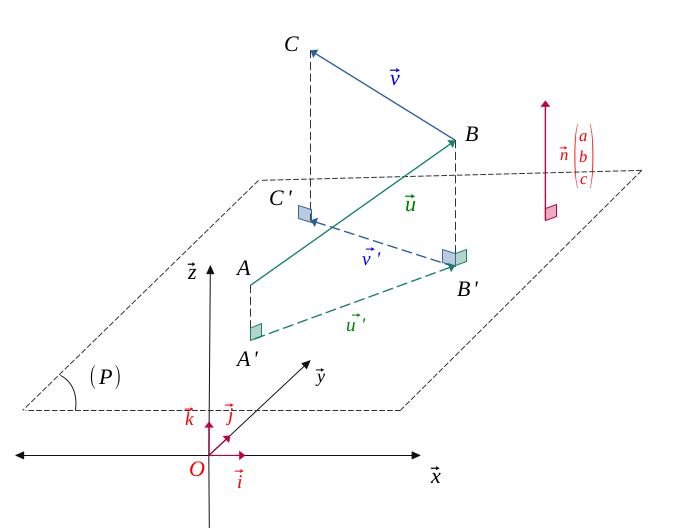
For the sake of simplicity, we placed the points $A, B, C$ as well as their respective projection $A', B', C'$.

Now, let $\vec{w} = \vec{u} + \vec{v}$, the sum of vectors $\vec{u}$ and $\vec{v}$, and the vector $\vec{w'}$ being the projection of $ \vec{w}$ on this plane.

Projection of the sum of two vectors upon a plane

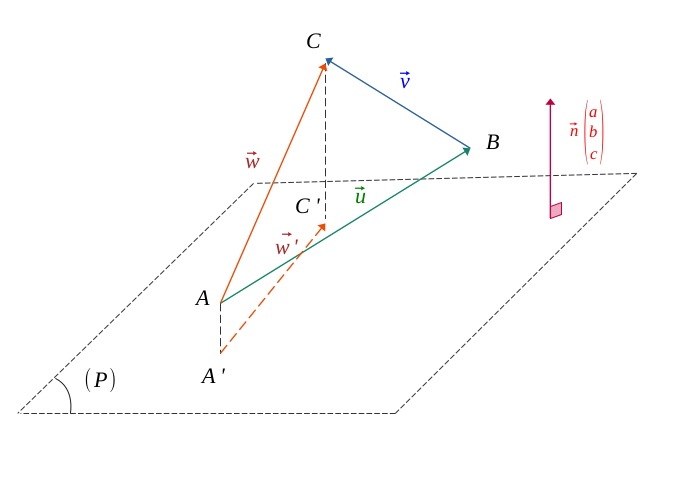
In the case of the initial points $A, B, C$ and those of their respective projection $A', B', C'$, the Chasles relation applied:

$$ \Biggl \{ \begin{gather*} \vec{u} + \vec{v} = \vec{w} \\ \vec{u}' + \vec{v}' = \ \vec{w}' \end{gather*} $$

Therefore,

The projection of a sum of vectors is the sum of each vector's projection

$$ \forall n \in \mathbb{N}, \ \forall (\vec{u_1}, \vec{u_2}, \ ..., \vec{u_n}), $$

$$ proj\left(\sum_{k=0}^n \overrightarrow{ u_k} \right) = \sum_{k=0}^n proj(\overrightarrow{u_k})$$

Geometrical figures

Equation of a sphere

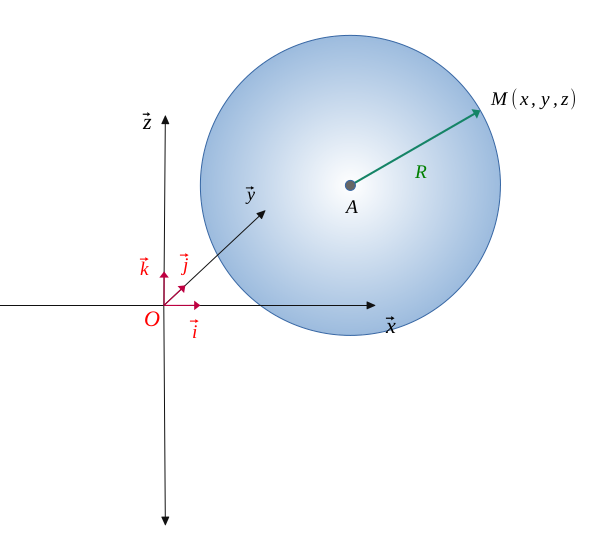
Let $(\mathcal{S})$ be a sphere having a radius $R$ and centered at point $A(x_0, y_0, z_0)$.

On this sphere, every point every point $M\bigl[x, y, z \bigr]$ is equidistant from the point $A$, which is worth the length of the radius $R$.

We know that using the the Pythagorean theorem, that the distance $ AB$ in a three-dimensional space is worth:

$$\forall (A, B) \in \hspace{0.05em} (O, \vec{x}, \vec{y}, \vec{z})^2, $$

$$AB =\sqrt{(x_b - x_a)^2 + (y_b - y_a)^2 + (z_b - z_a)^2 }$$

So,

$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} AM = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 }$$

$$ R = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 }$$

$$ R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$

The sphere $(\mathcal{S})$ of radius $R$ and centered at point $A(x_0, y_0, z_0)$ has for equation in space:

$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$

$$ (with \enspace (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3) $$

Equation of a cylinder

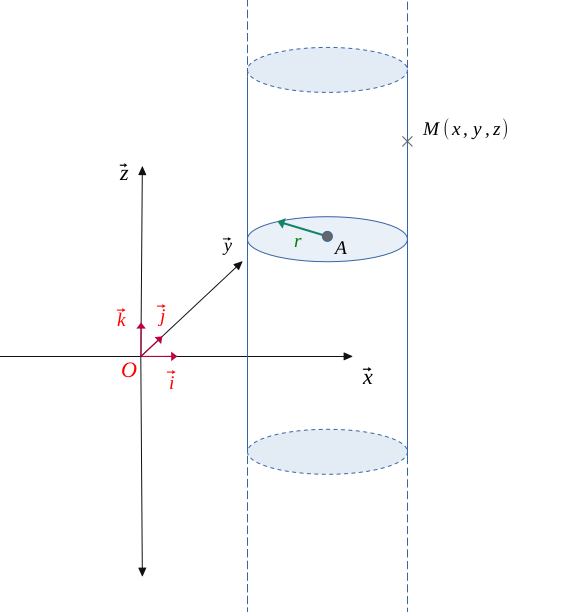
Let $(\mathcal{C})$ be a vertical cylinder of radius $r$ and centered at point $A(x_0, y_0, z_0)$.

In the plane $(O, \overrightarrow{i}, \overrightarrow{j})$, the cylinder describes a circle.

We know that using the the Pythagorean theorem, that the distance $ AB$ in a plane is worth:

$$\forall (A, B) \in \hspace{0.05em} (O, \vec{x}, \vec{y})^2, $$

$$AB = \sqrt{ (x_b - x_a)^2 + (y_b - y_a)^2} $$

We then have,

$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} AM = \sqrt{(x-x_0)^2 + (y-y_0)^2 }$$

$$ r = \sqrt{(x-x_0)^2 + (y-y_0)^2 }$$

$$ r^2 = (x-x_0)^2 + (y-y_0)^2 $$

The vertical axis $z$ can take any value, so it is a free variable.

The cylinder $(\mathcal{C})$ having a radius $r$ and centered at point $A(x_0, y_0, z_0)$ has for equation in space:

$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} r^2 = (x-x_0)^2 + (y-y_0)^2 $$

$$ (with \enspace (x_0, y_0) \in \hspace{0.05em} \mathbb{R}^2) $$

Equation of a cone

Let $(\mathcal{C})$ a vertical cone have as half-angle $ \theta$, and centered at point $A(x_0, y_0, z_0)$.

In the figure below, we can see that:

$$ M \in \mathcal{C}(A, \theta) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} tan(\theta) = \frac{AM'}{AM} $$

$$ \Longleftrightarrow \hspace{0.1em} tan(\theta) = \frac{\sqrt{ (x- x_0)^2 + (y- y_0)^2} }{|z-z_0|} $$

$$ tan^2(\theta) = \ \frac{ (x- x_0)^2 + (y- y_0)^2 }{(z-z_0)^2} $$

$$ (x- x_0)^2 + (y- y_0)^2 = (z-z_0)^2 tan^2(\theta) $$

The cone $(\mathcal{C})$ have as half-angle $ \theta$, and centered at point $A(x_0, y_0, z_0)$ $A(x_0, y_0, z_0)$ has for equation in space:

$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} (x- x_0)^2 + (y- y_0)^2 = k(z-z_0)^2 $$

$$ with \enspace \Biggl \{ \begin{gather*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ k = tan^2(\theta) \end{gather*} $$

Coordinates system

From cartesian to spherical coordinates

In some cases, it can be useful to use spherical coordinates (in two dimensions : polar coordinates), especially when working with spheres.

Longitude-latitude coordinates

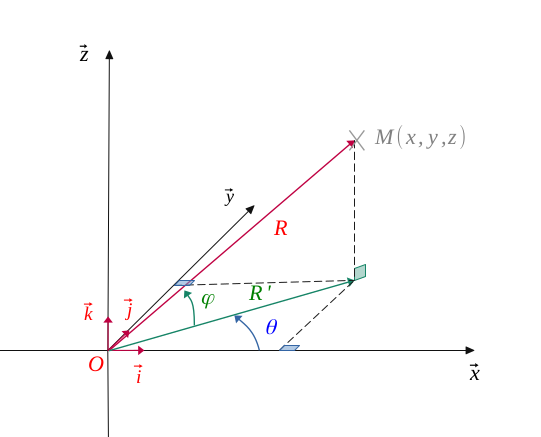
In a usual orthonormal reference frame in space $(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})$, we represented a point $M\bigl[x, y, z \bigr]$.

Let $R$ representing the distance from this point to the origin and $R'$ its projection on the horizontal plane $(O, \overrightarrow{i}, \overrightarrow{j})$.

Likewise, we called $\theta$ the angle formed by the abscissa axis $(O, \overrightarrow{i})$ and $R'$, and also $\varphi$ the angle formed $R'$ and $R$.

$$ \Biggl \{ \begin{gather*} \theta = (\overrightarrow{Ox}, \overrightarrow{R'}) \\ \varphi= (\overrightarrow{R'}, \overrightarrow{R})\end{gather*} $$

In the following figure, we have represented the point $M'$, projection of point $M$ on the horizontal plane $(O, \overrightarrow{i}, \overrightarrow{j})$.

Calculation of the projection of R on the horizontal plane

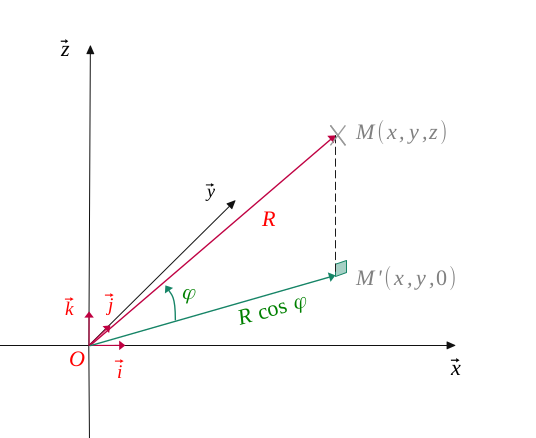
With the classic trigonometry rules, we easily see that:

$$ \Biggl \{ \begin{gather*} z = R \ sin(\varphi) \\ R' = R \ cos(\varphi) \end{gather*} $$

Now, working with a front view of the horizontal plane $(O, \overrightarrow{i}, \overrightarrow{j})$, we can calculate the coordinates corresponding to $x$ and $y$.

Calcul of x and y on the horizontal plane

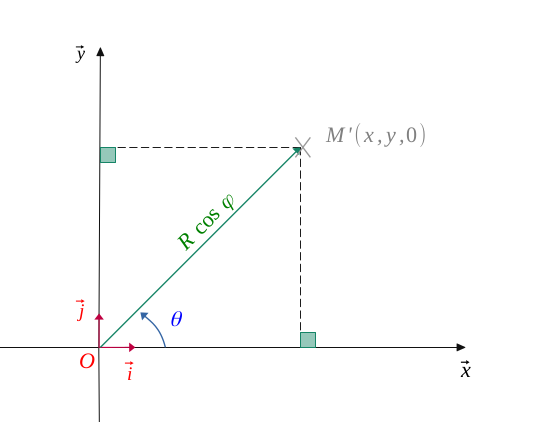
We do have :

$$ \Biggl \{ \begin{gather*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \end{gather*} $$

Finally, the distance $R$ is easily calculated from cartesian coordinates $(x, y, z)$:

$$R =\sqrt{x^2 +y^2 +z^2 }$$

As well, we obtain both angles $\theta$ and $\varphi$ by:

$$ \Biggl \{ \begin{gather*} \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{gather*} $$

So,

$$ \Biggl \{ \begin{gather*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \\ z = R \ sin(\varphi) \end{gather*} \qquad (\theta : longitude- \varphi : latitude) $$

$$with \enspace \left \{ \begin{gather*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{gather*} \right \}$$

Longitude-colatitude coordinates

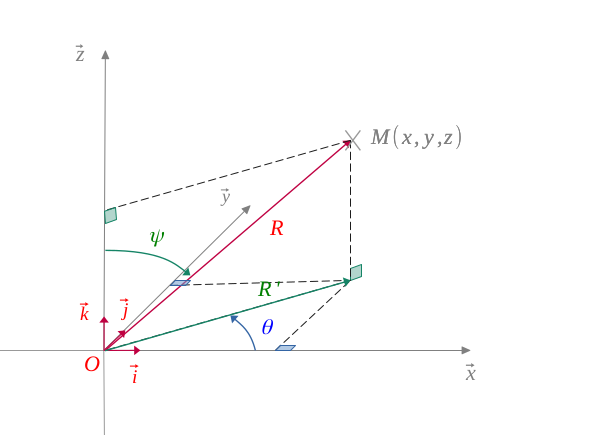
here is another way to represent spherical coordinates; we can use colatitude instead of latitude.

We then have a new angle $\psi$ which starts from the vertical axis $\overrightarrow{Oz}$ towards $R$ in the antitrigonometric direction.

$$ \Biggl \{ \begin{gather*} \theta = (\overrightarrow{Ox}, \overrightarrow{R'}) \\ \varphi= (\overrightarrow{Oz}, \overrightarrow{R})\end{gather*} $$

Which gives us, applying the same reasoning:

$$ \Biggl \{ \begin{gather*} x = R \ sin(\psi) \ cos(\theta) \\ y = R \ sin(\psi) \ sin(\theta) \\ z = R \ cos(\psi) \end{gather*} \qquad (\theta : longitude- \psi : colatitude) $$

$$with \enspace \left \{ \begin{gather*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \psi = arccos \left( \frac{z}{R} \right) \end{gather*} \right \}$$

Examples

Intersection between two planes$: \mathcal{P} \cap \mathcal{P}' $

Let us find the intersection $(\mathcal{P} \cap \mathcal{P}') $ between the two planes $(\mathcal{P}) $ and $(\mathcal{P}') $.

$$ (\mathcal{S}) \ \Biggl \{ \begin{gather*} \ \ 3x \ - \ y \ + z \hspace{1.8em}= 0 \qquad (\mathcal{P}) \\ -2x +2y + z + 1 = 0 \qquad (\mathcal{P}') \end{gather*} $$

We scale the system $(\mathcal{S})$ performing the linear combination $ 2(\mathcal{P}) $ + $ 3(\mathcal{P}') $.

$$ (\mathcal{S}) \ \Biggl \{ \begin{gather*} 3x - y \ + z = 0 \hspace{5em} (\mathcal{P}) \\ \ \ \ \ 4y +5 z = -3 \qquad \qquad (2(\mathcal{P}) + 3(\mathcal{P}') ) \end{gather*} $$

The system is of the rank $2$, then the intersection is a straight line which we will note $ (\mathcal{D})$. Moreover, the parameter $ z $ is a free variable and:

$$z = \frac{4y-3}{5} \Longleftrightarrow y = \frac{-5z-3}{4} $$

So, we solve the system by going backwards and we find:

$$ \left \{ \begin{gather*} x = \frac{-3z-1}{4} \\ y = \frac{-5z-3}{4} \\ z= z \end{gather*} \right \} $$

We choose as value $ z = 0 $ to fix a point on the line $ (\mathcal{D})$. So $ A\left(-\frac{1}{4},-\frac{3}{4}, 0 \right) \in \mathcal{D}$.

Furthermore, we see that the vector $\vec{u}\begin{pmatrix} -\frac{3}{4} \\ - \frac{5}{4} \\ \hspace{1em} 1 \end{pmatrix}$ leads the straight line $ (\mathcal{D})$, then the latter has the equation:

$$ M\bigl[x, y, z \bigr] \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x + \frac{1}{4} = -\frac{3}{4}t\\ y + \frac{3}{4} = -\frac{5}{4}t \\z = t \end{Bmatrix} $$

So,

$$(\mathcal{P} \cap \mathcal{P}')=(\mathcal{D}) \Longleftrightarrow \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x = -\frac{3}{4}t - \frac{1}{4}\\ y = -\frac{5}{4}t -\frac{3}{4} \\z = t \end{Bmatrix} $$

Intersection between a line and a plane $: \mathcal{D} \cap \mathcal{P} $

Let us find the intersection $(\mathcal{D} \cap \mathcal{P}) $ between a line $(\mathcal{D}) $ and a plane $(\mathcal{P}) $.

$$ (\mathcal{D}) \ \Biggl \{ \begin{gather*} x = t-1 \\ y = -2t + 3 \\ z= -t+5 \end{gather*} $$

$$ 2x + y -3z + 6 = 0 \qquad (\mathcal{P})$$

We inject the coordinates of $(\mathcal{D}) $ in those of $(\mathcal{P}) $, and we solve $(L) $ :

$$ 2(t-1) -2t + 3 -3(-t+5) + 6 = 0 \qquad (L)$$

$$ 2t-2-2t+3+3t -15 +6 = 0 \qquad (L)$$

$$ 3t-8 = 0 \Longleftrightarrow t = \frac{8}{3} \qquad (L)$$

As $t $ is unique, there is a point of intersection, which we will note $A$.

We thus determine this point using the parametric equation of the line $(\mathcal{D}) $.

Then this point of intersection is:

$$ (\mathcal{D} \cap \mathcal{P}) = A\left(\frac{5}{3}; -\frac{7}{3}; \frac{7}{3} \right)$$

Intersection between two lines$: \mathcal{D} \cap \mathcal{D}' $

Let us find the intersection $(\mathcal{D} \cap \mathcal{D}') $ between two lines $(\mathcal{D}) $ and $(\mathcal{D}') $.

$$ (\mathcal{D}) \ \Biggl \{ \begin{gather*} x = 2t-1 \\ y = -t-2 \\ z= t+2 \end{gather*} $$

$$ (\mathcal{D}') \ \Biggl \{ \begin{gather*} x = s+1 \\ y = 3s-1\\ z= 2s+1\end{gather*} $$

We do the following system:

$$ (\mathcal{D} \cap \mathcal{D}') \ \Longleftrightarrow \Biggl \{ \begin{gather*} 2t-1 = s+1 \\ -t-2 = 3s-1\\ t +2 = 2s+1\end{gather*} $$

$$ (\mathcal{D} \cap \mathcal{D}') \ \Longleftrightarrow \ \Biggl \{ \begin{gather*} 2t-s = 5 \ \ \qquad (L_1) \\ -t-3s = 1 \qquad (L_2) \\ t-2s = -1 \qquad (L_3) \end{gather*} $$

We first solve the first two equations. We carry out $ (L_1 + 2 L_2)$:

$$-7s = 7 \qquad (L_1 + 2 L_2) \ \Longrightarrow \ s = -1 \ \Longrightarrow \ t = 2 $$

This solution is not suitable for the third one $ (L_3)$ because:

$$2 - 2\times(-1) = 4\neq -1 $$

So, as there is no pair $ (t, s) \in \hspace{0.05em} \mathbb{R}^2$ which are suitable for the two parametric equations of the two lines $(\mathcal{D}) $ and $(\mathcal{D}') $, they have no point of intersection.

$$(\mathcal{D} \cap \mathcal{D}') = \emptyset $$

Intersection between a plane and a sphere $ : \mathcal{P} \cap \mathcal{S} $

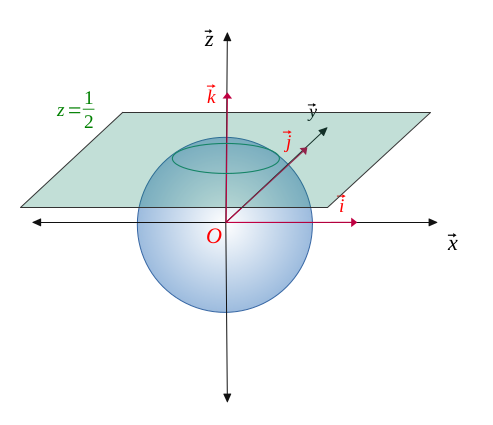
Let us find the intersection $(\mathcal{P} \cap \mathcal{S}) $ between a plane$(\mathcal{P}) $ and a sphere $(\mathcal{S}) $.

$$ z = \frac{1}{2} \qquad (\mathcal{P}) $$

$$ x^2 + y^2 + z^2 = 1 \qquad (\mathcal{S}) $$

We now inject $(\mathcal{P}) $ into $(\mathcal{S}) $:

$$ x^2 + y^2 = \frac{3}{4} $$

So, we get an equation for the coordinates $(x,y) \in \hspace{0.05em} \mathbb{R}^2 $. On the other hand, it is the equation of a cone of radius $R = \frac{\sqrt{3}}{2}$, so it is then necessary to keep the equation of the plane $(\mathcal{P}) $ to fix the cone and therefore obtain a circle.

So, the intersection between $(\mathcal{P}) $ and $(\mathcal{S}) $ is modelled by the double equation:

$$ (\mathcal{P} \cap \mathcal{S}) \ \Longleftrightarrow \ \Biggl \{ \begin{gather*} x^2 + y^2 = \frac{3}{4} \\ z = \frac{1}{2} \end{gather*} $$

Intersection entre un plan et une sphère

Analytical geometry in space

Demonstrations

Lines and planes

Parametric equation of a straight line

Equation of a plane

Distance from a point to a plane

Projection of a sum of vectors upon a plane

Geometrical figures

Equation of a sphere

Equation of a cylinder

Equation of a cone

Coordinates system

From cartesian to spherical coordinates

Examples

Intersection between two planes\(: \mathcal{P} \cap \mathcal{P}' \)

Intersection between a line and a plane \(: \mathcal{D} \cap \mathcal{P} \)

Intersection between two lines\(: \mathcal{D} \cap \mathcal{D}' \)

Intersection between a plane and a sphere \( : \mathcal{P} \cap \mathcal{S} \)