Solving third-degree equations (cubic equations)

A third degree equation is of the form:

Existence of obvious root(s)

If there are one or more obvious roots, then the polynomial can be factored and reduced to a lower degree.

Determination of the number of real roots according to the cases

After calculating the discriminant \(\Delta_3\) :

We do have the following number of real roots depending on the cases:

Resolution

1. if \( (\Delta_3 > 0) \)

• a simple real root

$$ X_1 = \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

• two complex roots

$$ C_2 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ C_3 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

And \( P_3(X) \) can be factorized as follows:

$$ P_3(X) = a(X - X_1)(X - C_2)(X - C_3) $$

2. if \( (\Delta_3 = 0) \)

• a simple real root

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

• a double real root

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

And \( P_3(X) \) can be factorized as follows:

$$ P_3(X) = a(X - X_1)(X - X_2)^2 $$

3. if \( (\Delta_3 < 0) \)

• three real roots

$$ X_1 = \sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + \sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$

Even though they appear in a complex form, after solving these solutions definitely become real.

And \( P_3(X) \) can be factorized as follows:

$$ P_3(X) = a(X - X_1)(X - X_2)(X - X_3) $$

---

Démonstration

A third degree equation is of the form:

So, we are trying to solve:

Existence of obvious root(s)

If there are one or more obvious roots, then the polynomial can be factored and reduced to a lower degree.

Determination of the number of real roots according to the cases

In the general case, we can use a graphical approach to determine the number of roots according to the different cases.

We start from the equation \( (1) \) :

We factor by \( a \) :

From this point on, we will keep in mind that the general form \((2)\) contains \(a\) as a factor, but we will study the function inside the parenthesis:

We then seek to eliminate the second degree term.

The expression \((2^*)\) then becomes:

We will then study the function \((f)\):

Let us note from now on that \(f\) is an odd function, being the sum of odd functions.

Next, let's try to derive this function:

Let's factor this derivative \(f'\).

And let us seek these roots:

Let there be two roots:

So, we can rewrite it in its factorized form:

As the function \(f\) change de sens de variations changes direction of variations before \(\chi_1\) and after \(\chi_2\), it therefore has two inflection point in \(\chi_1\) and \(\chi_2\).

And as we know that \( P_3(\chi)\) is worth:

The variation table of \(P_3(\chi)\) will be that of \(f(\chi)\) if \((a > 0)\), but will be reversed if \((a < 0)\).

Let's look for the values of the images \( f\left(\chi_1 \right) \) and \( f\left(\chi_2 \right) \) :

To know the number of roots of \(f(\chi)\), we try to know the sign at a given instant of the product of these two images.

which we will call third-degree discriminant \(\Delta_3\):

We will then have three sub-cases to consider:

• \( \alpha) \) if \(\Delta_3 > 0 \)

If the discriminant is positive, this means that \(f\left(\chi_1\right)\) and \(f\left(\chi_2\right)\) are of the same sign, therefore:

• etiher both positive

According to the variation table of \(f\), there will be only one real root, located between \((\chi = -\infty)\) and \((\chi = \chi_1)\).

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$		$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$		$$ \textcolor{#4A8051}{f(\chi_2) > 0} $$		$$ + \infty $$


• or both negative

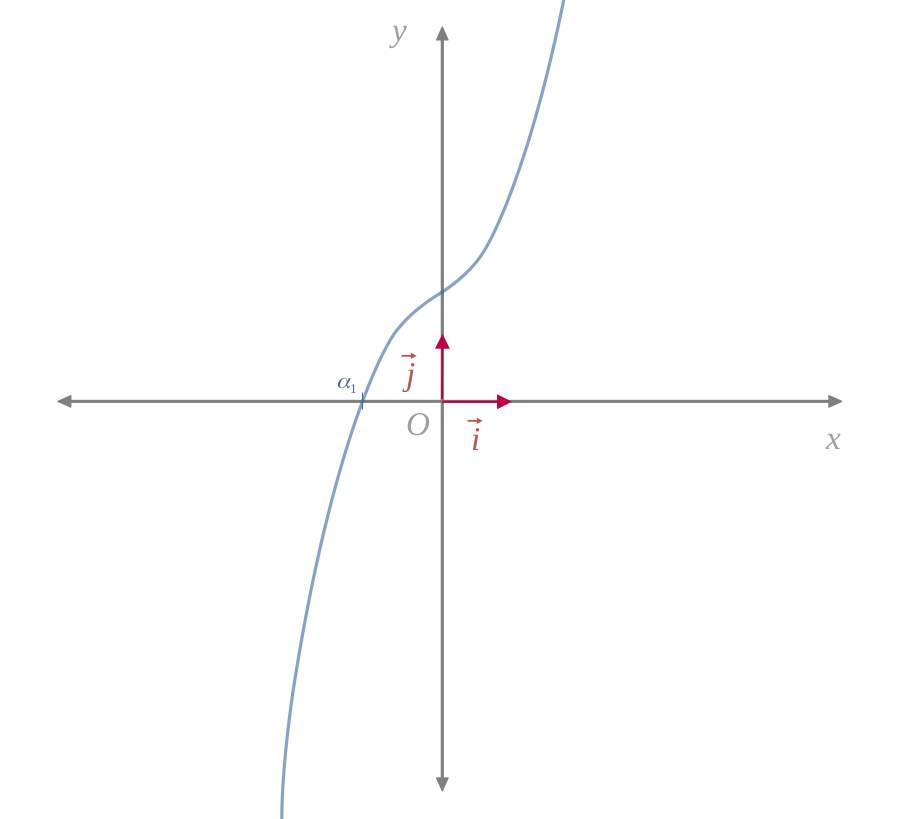
According to the variation table of \(f\), there will be only one real root, located between \((\chi = \chi_2)\) and \((\chi = +\infty)\).

$$ \chi $$	$$ -\infty $$		$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$		$$ \textcolor{#A45959}{f(\chi_1) < 0} $$		$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ + \infty $$

In both cases, there will be only one real root.

• \( \beta) \) if \( \Delta_3 = 0 \)

If the discriminant is zero, this means that one of the two images is zero, because according to the variation table, we always have:

$$ f(\chi_1) > f(\chi_2) $$
• \( f(\chi_1) = 0 \)

In this case, there will be a double root for \((\chi = \chi_1)\), and another root for \((\chi_2 < \chi < +\infty)\).

$$ \chi $$	$$ -\infty $$		$$ \textcolor{#6187B2}{\alpha_1 / \alpha_2 = \chi_1} $$		$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_3} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$		$$ \textcolor{#6187B2}{f(\chi_1) = 0} $$		$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\chi_2) = 0} $$	$$ + \infty $$


• \( f(\chi_2) = 0 \)

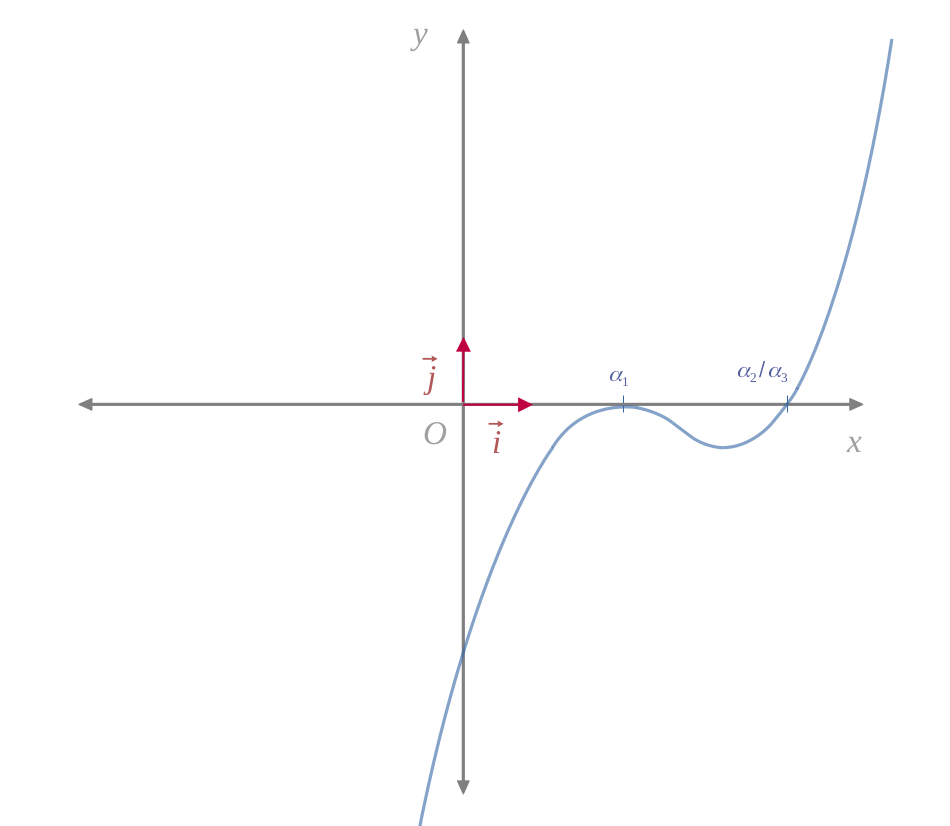
Dans ce cas symétrique, il y aura une racine simple pour \((\chi_2 < \chi < +\infty)\), ainsi qu'une racine double pour \((\chi = \chi_1)\).

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$		$$ \textcolor{#6187B2}{\alpha_2 / \alpha_3 = \chi_2} $$		$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$		$$ \textcolor{#6187B2}{f(\chi_2) = 0} $$		$$ + \infty $$



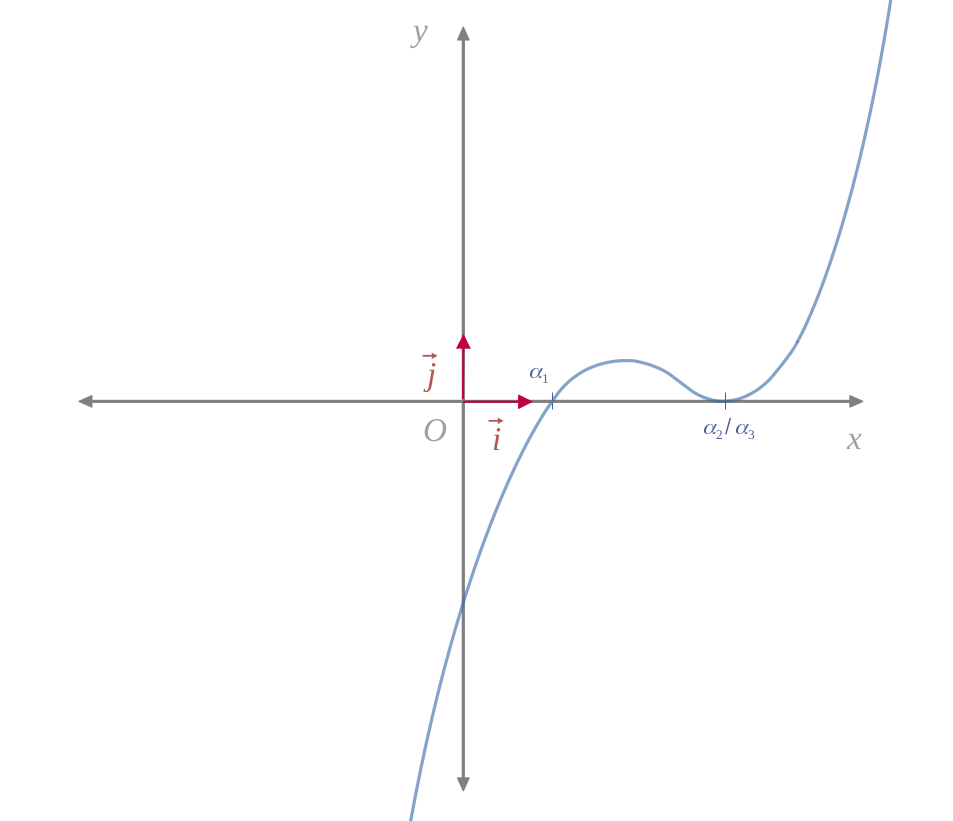
In both cases, we will have a double real root and a simple real root.

The double root necessarily lies on the plateau, because in the other case the function is strictly increasing.

• \( \gamma) \) if \( \Delta_3 < 0 \)

If the discriminant is negative, the two images \(f(\chi_1)\) et \(f(\chi_2)\) are of opposite signs.

As we know that:

$$ f(\chi_1) > f(\chi_2) $$

there is only one case, and we will distinguish three real roots.

$$ \chi $$	$$ -\infty $$	$$ \textcolor{#6187B2}{\alpha_1} $$	$$ \chi_1 = -\sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_2} $$	$$ \chi_2 = \sqrt{- \frac{p}{3}} $$	$$ \textcolor{#6187B2}{\alpha_3} $$	$$ +\infty $$
$$ f(\chi) = \chi^3 + p\chi + q $$	$$ - \infty $$	$$ \textcolor{#6187B2}{f(\alpha_1) = 0} $$	$$ \textcolor{#4A8051}{f(\chi_1) > 0} $$	$$ \textcolor{#6187B2}{f(\alpha_2) = 0} $$	$$ \textcolor{#A45959}{f(\chi_2) < 0} $$	$$ \textcolor{#6187B2}{f(\alpha_3) = 0} $$	$$ + \infty $$


• \( \delta) \) summary

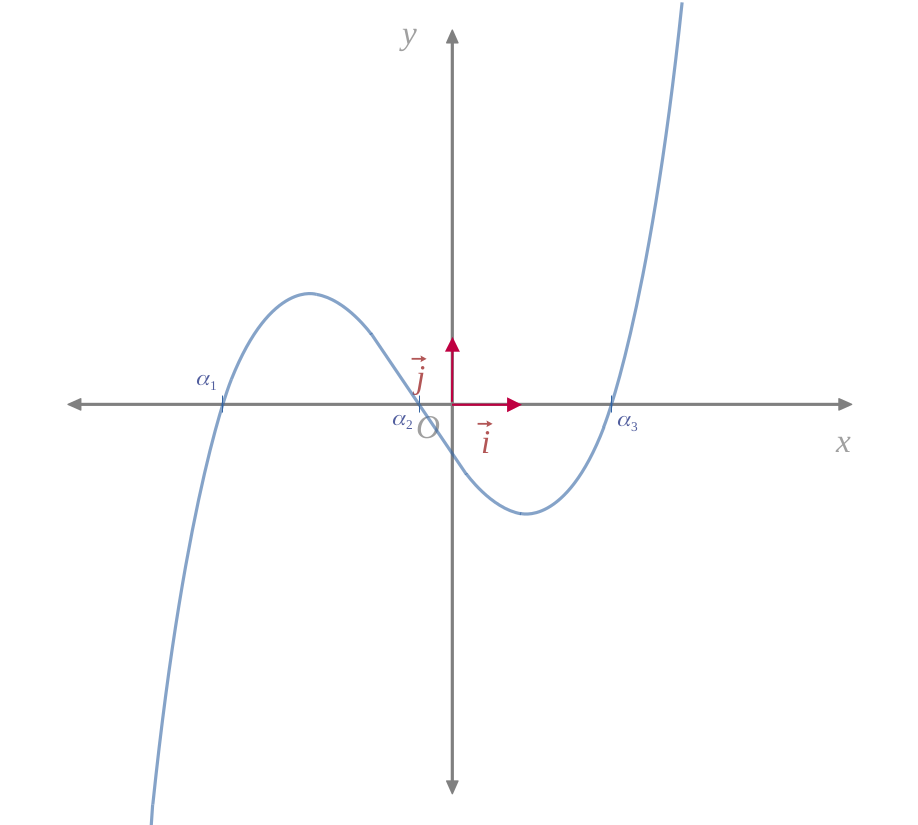
In summary, here are the cases according to the result of the discriminant \(( \Delta_3 = q^2 + \frac{4p^3}{27} )\):

Sign of the discriminant \( \Delta_3 \)	Numbers of roots
$$ \Delta_3 > 0 $$	1 real root
$$ \Delta_3 = 0 $$	3 real roots (including one double)
$$ \Delta_3 < 0 $$	3 real roots

Resolution

Let's briefly summarize the path taken in the previous point. We started from the equation to be solved \((1)\):

Then, we factorized by \(a\) :

The \(a\) factor not changing the roots, we can get rid of it:

and make a first change of variable.

We then arrived at:

Which gives us:

We develop the expression:

Now multiplying by \(w^3\), we obtain that:

We now have a second-degree equation by once again introducing a new variable:

So, the expression\((4^*)\) now becomes:

With this second-degree equation, we can calculate the second degree discriminant, which we will call as above \(\Delta_3\) :

1. if \( (\Delta_3 > 0) \)

With the equation \((5)\):

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

If \( (\Delta_3 > 0) \), we obtain two real solutions:

$$ z_1 / z_2 = \frac{- q \pm \ \sqrt{\Delta_3}}{2} $$
$$ \Bigl(with \ \Delta_3 = q^2 + \frac{4p^3}{27} \Bigr) $$

Which can be arranged in:

$$ z_1 / z_2 = -\frac{q}{2} \pm \frac{ \sqrt{q^2 + \frac{4p^3}{27}}}{2} $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \frac{ \sqrt{q^2 + \frac{4p^3}{27}}}{\sqrt{4}} $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \sqrt{\frac{q^2}{4} + \frac{p^3}{27} } $$
$$ z_1 / z_2 = -\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } $$

We made these different variable changes as a result:

$$ \left[ X = \chi - \frac{b}{3a} \right] \ puis \ \biggl[ \chi = w - \frac{p}{3w} \biggr] \ puis \ \Bigl[ w^3 = z \Bigr] $$

You must therefore reassemble them in the opposite direction:

$$ \Bigl[ z \longmapsto w \Bigr] \ puis \ \Bigl[ w \longmapsto \chi \Bigr] \ puis \ \Bigl[ \chi \longmapsto X \Bigr] $$
1. \(z \longmapsto w \)

Taking the cube root of \(z\), we will have as coefficient the three roots of unity which are three unit roots of a complex number which are \( \Bigl \{1, \ e^{\frac{2i\pi}{3}}, \ e^{-\frac{2i\pi}{3}} \Bigr \} \), which gives us six roots in all:

$$ w_1 / w_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ w_3 / w_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ w_5 / w_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
2. \(w \longmapsto \chi \)

The six expressions then become:

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$
$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3 e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p}{3 e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} $$

Then, we multiply the numerators and denominators by their respective conjugates.

For the first pair of solutions \(\chi_1 / \chi_2 \):

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} }{3\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }}} } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 - \left(\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right) } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{\underbrace{\left(\frac{q}{2} \right)^2 - \left(\frac{q}{2}\right)^2 } _\text{= 0} - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{3\sqrt[3]{ \left(- \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} - \frac{p \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} }{-\frac{3p}{3}} $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

These two roots are actually one, because of double signs \(\pm\) and \(\mp \) present in each of the first two terms:

$$ \chi_1 = \chi_2 = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

For the other two pairs of solutions \((\chi_3 / \chi_4, \ \chi_5 / \chi_6)\), we follow the same approach, and after calculations we arrive at the following forms:

$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$

For them too, we can group them together because they are two by two identical:

$$ X_3 = X_6 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
$$ X_4 = X_5 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} $$
3. \(\chi \longmapsto X \)

For this last step, we just have to add to each solution the term \(-\frac{b}{3a}\).

$$ X_1 = X_2 = \sqrt[3]{-\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + \sqrt[3]{-\frac{q}{2} \mp \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
$$ X_3 = X_6 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
$$ X_4 = X_5 = e^{\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} + e^{-\frac{2i\pi}{3}} \ \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 }} -\frac{b}{3a} $$
4. conclusion

We saw this equality above:

$$ \frac{- q \pm \ \sqrt{\Delta_3}}{2} = -\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } $$

So, we put this equality back in place for the presentation of the solutions.

In this case of \( (\Delta_3 > 0) \) we then have that:

• a simple real root

$$ X_1 = \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$

• two complex roots

$$ C_2 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ C_3 = e^{\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q + \sqrt{\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}} \ \ \sqrt[3]{\frac{-q - \sqrt{\Delta_3}}{2}} - \frac{b}{3a} $$
$$ with \ \left(\Delta_3 = q^2 + \frac{4p^3}{27} \right) $$
$$ et \ \left \{ \begin{gather*} p = \frac{-b^2 + 3ac}{3a^2} \\ \\ q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \end{gather*} \right \} $$

Hence, the polynomial \(P_3(X)\) admits the following factorization:

$$ P_3(X) = a(X - X_1)(X - C_2)(X - C_3) $$
2. if \( (\Delta_3 = 0) \)

With the equation \((5)\):

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

if \( (\Delta_3 = 0) \), we have a real double solution:

$$ z_0 = -\frac{q}{2} $$

In the same way as above, we go back through the different variable changes one after the other.

1. \(z \longmapsto w \)
$$ w_1 = \sqrt[3]{-\frac{q}{2}} $$
$$ w_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ w_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
2. \(w \longmapsto \chi \)

For the fisrt solution \(\chi_1 \):

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3\sqrt[3]{-\frac{q}{2}}}$$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3\sqrt[3]{-\frac{q}{2}}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\textcolor{#A45959}{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}}{\sqrt[3]{-\frac{q}{2}} \textcolor{#A45959}{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$

But as:

$$ \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = \frac{\Delta_3}{2} $$

(voir plus haut)

And that we have as hypothesis that \( \Delta_3 = 0 \), then:

$$\Delta_3 = 0 \Longrightarrow 2 \sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = 0 $$

And so that:

$$\sqrt{\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 } = 0 $$

Which also implies that:

$$\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 = 0 $$

$$\left(\frac{q}{2}\right)^2 = - \left( \frac{p}{3} \right)^3 $$

$$\sqrt[3]{ \left(\frac{q}{2}\right)^2 } = \sqrt[3]{ - \left( \frac{p}{3} \right)^3 } $$

$$\sqrt[3]{ \left(\frac{q}{2}\right)^2 } = -\frac{p}{3} $$

We can then replace in the previous expression:

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} - \frac{p}{3}\frac{\sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \frac{ \sqrt[3]{ \left(\frac{q}{2}\right)^2 } \sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \frac{ \sqrt[3]{ \left(-\frac{q}{2}\right)^2 } \sqrt[3]{\left(-\frac{q}{2} \right)^2}}{-\frac{q}{2}} $$

Now, we can make the power formulas work:

$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \left(-\frac{q}{2}\right)^{\frac{4}{3}} \left(-\frac{q}{2}\right)^{-1 } $$
$$ \chi_1 = \sqrt[3]{-\frac{q}{2}} + \left(-\frac{q}{2}\right)^{\frac{1}{3}} $$
$$ \chi_1 = 2\sqrt[3]{-\frac{q}{2}} $$

For the other two solutions:

$$ w_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ w_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_3 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$

These two solutions are one and the same solution:

$$ \chi_2 = \chi_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2}} $$
$$ \chi_2 = \chi_3 = \sqrt[3]{-\frac{q}{2}} \left(e^{\frac{2i\pi}{3}} + e^{-\frac{2i\pi}{3}} \right) $$
$$ \chi_2 = \chi_3 = -\sqrt[3]{-\frac{q}{2}} $$
3. \(\chi \longmapsto X \)
$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
4. conclusion

In this case of \( (\Delta_3 = 0) \) we then have that:

• a simple real root

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$

• a double real root

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ with \ \left(q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \right) $$

Hence, the polynomial \(P_3(X)\) admits the following factorization:

$$ P_3(X) = a(X - X_1)(X - X_2)^2 $$
3. if \( (\Delta_3 < 0) \)

With the equation \((5)\):

$$ z^2 + qz - \frac{p^3}{27} = 0 \qquad (5) $$

If \( (\Delta_3 < 0) \), we do obtain two complex solutions:

$$ z_1 = \frac{- q \pm i\sqrt{|\Delta_3|}}{2} $$

Which can be arranged as previously in:

$$ z_1 / z_2 = -\frac{q}{2} \pm i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| } $$

In the same way as above, we go back through the different variable changes one after the other.

1. \(z \longmapsto w \)
$$ w_1 / w_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ w_3 / w_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ w_5 / w_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
2. \(w \longmapsto \chi \)

The six expressions then become:

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$
$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3 e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}} \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p}{3 e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} $$

For the first couple of solutions \(\chi_1 / \chi_2 \):

$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} }{3\sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} \textcolor{#A45959}{\sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }}} } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 + \left|\left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\left( -\frac{q}{2} \right)^2 + -\left(\frac{q}{2}\right)^2 - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{\underbrace{\left(\frac{q}{2} \right)^2 + -\left(\frac{q}{2}\right)^2} _\text{ = 0 } - \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{3\sqrt[3]{- \left( \frac{p}{3} \right)^3 } } $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{p \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} }{-\frac{3p}{3}} $$
$$ \chi_1 / \chi_2 = \sqrt[3]{-\frac{q}{2} \ \pm \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ \mp\ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$

These two solutions are one and the same solution.

$$ \chi_1 = \chi_2 = \sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$

For the other two pairs of solutions \((\chi_3 / \chi_4, \ \chi_5 / \chi_6)\), we follow the same approach, and after calculations we arrive at the following forms:

$$ \chi_3 / \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
$$ \chi_5 / \chi_6 = e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} $$
3. \(\chi \longmapsto X \)
$$ X_1 = X_2 = \sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + \sqrt[3]{-\frac{q}{2} \ - i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
$$ \chi_3 = \chi_4 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
$$ \chi_5 = \chi_6 = e^{\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ - \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} + e^{-\frac{2i\pi}{3}}\sqrt[3]{-\frac{q}{2} \ + \ i\sqrt{\left| \left(\frac{q}{2}\right)^2 + \left( \frac{p}{3} \right)^3 \right| }} - \frac{b}{3a} $$
4. conclusion

In the same way as above, we get rid of the absolute value in the presentation of the results.

In this case of \( (\Delta_3 < 0) \) we then have that:

• three real roots

$$ X_1 = \sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + \sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_2 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ X_3 = e^{\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ - \ i\sqrt{-\Delta_3}}{2}} + e^{-\frac{2i\pi}{3}}\sqrt[3]{\frac{-q \ + \ i\sqrt{-\Delta_3}}{2}} - \frac{b}{3a} $$
$$ with \ \left(\Delta_3 = q^2 + \frac{4p^3}{27} \right) $$
$$ et \ \left \{ \begin{gather*} p = \frac{-b^2 + 3ac}{3a^2} \\ \\ q = \frac{2b^3 + 27a^2d - 9abc}{27a^3} \end{gather*} \right \} $$

Even if they appear in complex form, after solving these solutions definitely become real.

Hence, the polynomial \(P_3(X)\) admits the following factorization:

$$ P_3(X) = a(X - X_1)(X - X_2)(X - X_3) $$

---

Examples

1. Existence of obvious root(s)

$$ P_3(X) = X^3 + X^2 + X + 1 $$

We do notice that \( (X = -1) \) is an obvious root. Let us try to find the second-degree polynomial having coefficients \((\alpha, \beta, \gamma)\) such as:

$$ P_3(X) = (X + 1)(\alpha X^2 + \beta X + \gamma) $$

Let us make a polynomial division to find it:

$$$$	$$ X + 1 $$
$$\hspace{1em} X^3 + X^2 + X + 1 $$	$$ \textcolor{#608742}{X^2} $$
$$ \textcolor{#AF5F5F}{-X^3} \textcolor{#AF5F5F}{-X^2} + X + 1 $$	$$ X^2 $$
$$ \hspace{1em} 0 \hspace{1.2em} + \hspace{0.2em} 0 \hspace{0.4em} \textcolor{#AF5F5F}{-X - 1} $$	$$ X^2 \textcolor{#608742}{+ 1} $$

As a result,

$$ P_3(X) = (X + 1)(X^2 + 1) $$

We now seek its roots.

$$ \Delta = 0^2 - 4 \times 1 \times 1$$
$$ \Delta = -4 $$

As \(\Delta\) is negative, there is two complex roots:

$$ C_1 = \frac{- 0 - i\sqrt{-(-4)}}{2 \times 1} $$
$$ C_1 = -i $$
$$ C_2 = \frac{- 0 + i\sqrt{-(-4)}}{2 \times 1} $$
$$ C_2 = i $$

So, the solution of \( \Bigl[ P_3(X) = 0 \Bigr] \) are:

$$ \mathcal{S} = \biggl \{X_{1} = -1 , \ C_{2} = -i, \ C_{3} = i \biggr \} $$

\(P_3(X) \) can than be factorized as follows:

$$ P_3(X) = (X + 1)(X + i)(X - i) $$

2. Case of a discriminant equal to zero

$$ Q_3(X) = X^3 - 5X^2 + 8X - 4 $$

We compute the third-degree discriminant \(\Delta_3\):

$$ \Delta_3 = q^2 + \frac{4p^3}{27}$$
$$ \Delta_3 = \left(\frac{2b^3 + 27a^2d - 9abc}{27a^3}\right)^2 + \frac{4\left(\frac{-b^2 + 3ac}{3a^2}\right)^3}{27} $$
$$ \Delta_3 = 0 $$

As \(\Delta\) is worth zero, we do have three real roots:

• a simple real root

$$ X_1 = 2\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_1 = 1 $$

• a double real root

$$ X_2 = X_3 = -\sqrt[3]{-\frac{q}{2}} - \frac{b}{3a} $$
$$ X_2 = X_3 = 2 $$

\(Q_3(X) \) can than be factorized as follows:

$$ Q_3(X) = (X - 1)(X - 2)^2 $$