Current

Other

Index

Printing

Derivativity of functions

Derivativity is key notion in analysis, because it underlies all physics and science in general.

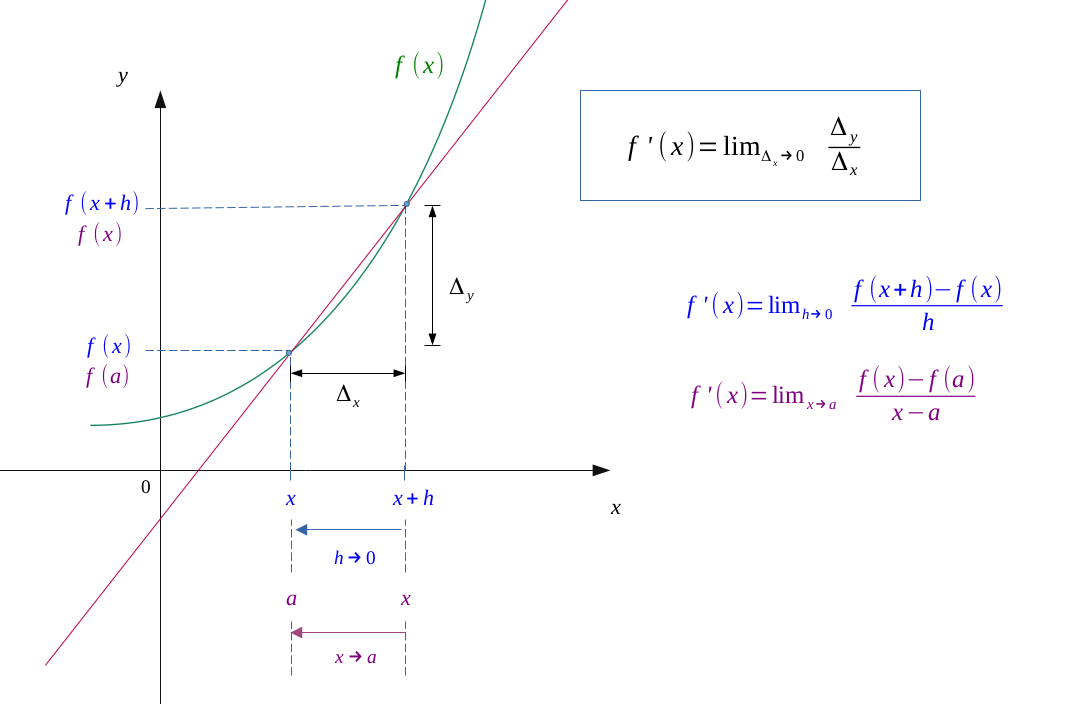
Let \( f :x \longmapsto f(x) \) be a continuous function.

1. Derived number

We do call \( f'(a) \) the derived number from the function \( f \) at point \( (x=a )\) such as

$$ f'(a) = \lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$

If (and only if) this number is defined, we then say that \( f \) is derivable at point \( a\).

$$ f \text{ is derivable at point } a \Longleftrightarrow \lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$

Determining the general expression of the derivative function \(f'\), we will define where the function \(f\) is derivable.

2. Derivative function

Function \(f'\), derivated from fucntion \( f \) is expressed as follows:

$$ f'(x) = \lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$

The is the limit of the rate variation when \( h \to 0 \).

It can also be found in this form:

$$ f'(x) = \lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$

At this point, it will be the limit of rate variation when \( x \to a \).

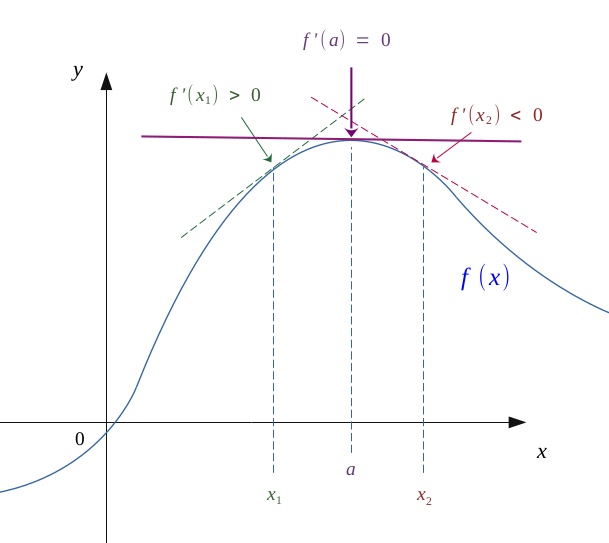
Furthermore, if and only if \(f'\) changes sign between before and after a certain point \(a\), the \(f\) function admits a local extremum at this point.

We saw in the definition of the derivative that the derived number correspond to the slope of the tangent to the curve of a function.

This line admits for equation at the point of abscissa \(a\):

Furthermore, in the case of a convex function (resp. concave), this tangent is always below (resp. above) the curve.

Demonstrations

The idea of derivativity

Let \( f :x \longmapsto f(x) \) be a function, continuous on an interval \( [a, \ a +h] \).

Let us mark two points on the abscissa axis, \( a \) and \( a +h \) (\( h \) being a relatively short distance). Their respective image being \( f(a) \) and \( f(a + h) \), we obtain two points: \( A(a; f(a)) \) and \( B(a + h; f(a + h)) \).

On the following figure, we also drawn the straight line joinin them.

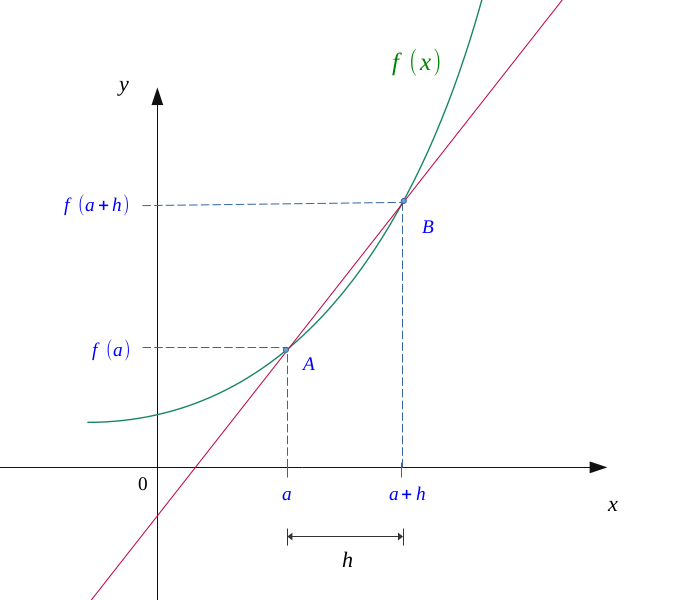
Now we can calculate a mean variation of this function between \( A \) and \( B \).

1. Derived number

1. Calculating the slope between \(A\) and \(B\)

We can calculate this slope by the following formula:

$$ m = \frac{ \Delta _y}{\Delta _x}$$

$$ m = \frac{ y_B- y_A}{x_B- x_A}$$



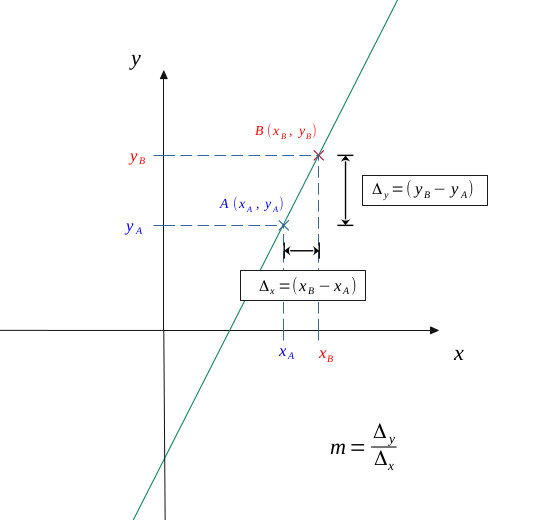
In our case, this gives:

$$ m = \frac{f(a+h) - f(a)}{ a + h -a} $$

So:

$$ m = \frac{f(a+h) - f(a)}{h} \qquad (1) $$
2. Shrinking of distance \(AB\)

Let us gradually reduce the distance \( h \) which separates our two points on the abscissa axis, making tend \(A\) towards \(B\).



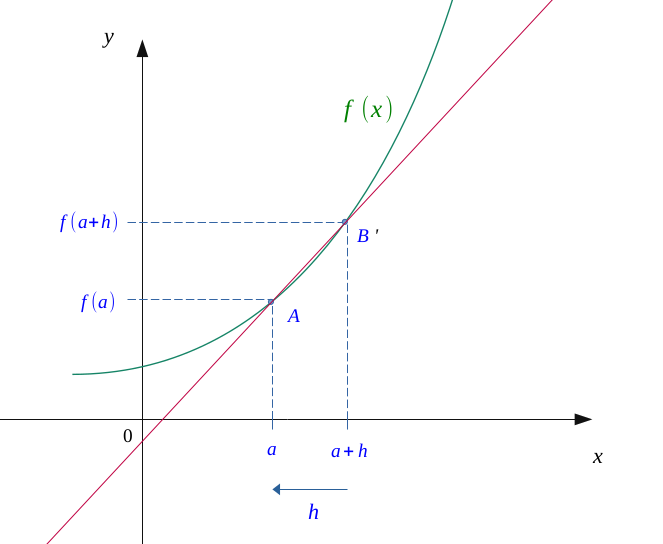
We see that the values of \( a \) and \( a + h \) started to get closer, and the line which connects \( A \) and \( B \) begin to draw a tangent to the curve.

3. Reduction to an infinitesimal distance

In the same way, we will further reduce the distance \( h \), the latter begins to reduce it to \( 0 \).



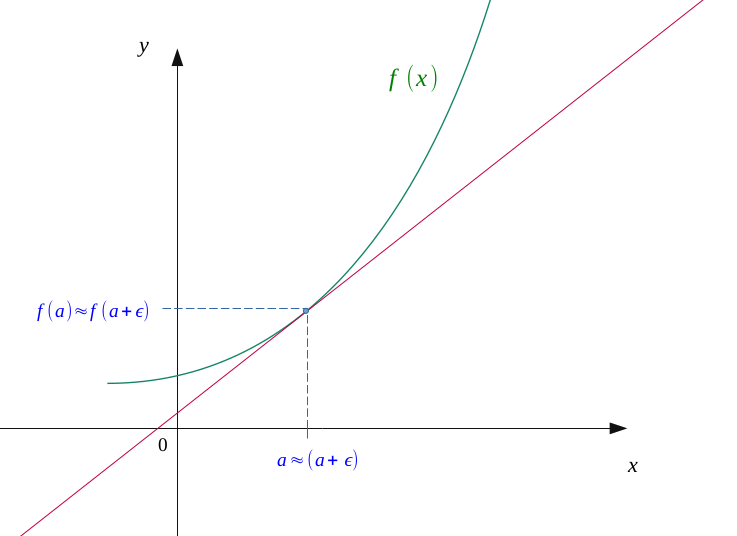
We now see that our two points \( A \) and \( B \) are almost coincident, and that we obtain an almost perfect tangent to the curve at the point of abscissa \( a \).

4. Derived number of a function at point \(a\)

By imaginating that \( h \) becomes smaller and smaller approching to \( 0 \), our formula \( (1) \) can be expressed as a limit:

$$ m = \lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h} $$

This number \( m\) obtained, for a \( a \) arbitrarily chosen, will be called the derived number of the function \( f \) at point \( a \). It will be noted \( f'(a) \).

$$ f'(a) = \lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$

If this number cannot be calculated, the derivative is not defined at this point \( a \).

Now, if (and only if) this number is defined, we will then say that \( f \) is derivable at point \( (x = a) \).

$$ f \text{ is derivable at point } a \Longleftrightarrow \lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$

Determining the general expression of the derivative function \(f'\), we will define where the function \(f\) is derivable.

2. Derivative function

By generalizing it, that is to say for all \( x \), we call \( f' \) the derivative function of the function \( f \).

$$ f'(x) = \lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$

The definition set of \( f' \) will then depend of its expression, and will be restricted to the definition set of the function \( f \).

For example, the function \( ln(x) \) is only defined on \(\mathbb{R^*_+}\).

Then, its derivative function:

$$ ln(x)' = \frac{1}{x} $$

is also restricted (a minima) to this interval, whereas the function \( f: x \longmapsto \frac{1}{x} \) is usually defined on \(\mathbb{R^*}\), which is a larger interval.

We say that the derivative is the limit of the variation rate when \( h \) goes to \( 0 \).

We will also find it through this form:

$$ f'(x) = \lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$

At this stage, it will be the limit of the variation rate when \( x \to a \).

In physics, we can also use Leibniz's differential notation \( \frac{df}{dx} \), or that of Newton \( \overset{.}{f} \).

Especially for integral calculus, it is convenient to use Leibniz's.

Derivativity implies continuity

We saw above that if a function can be derivated at point \( a\), tehen:

And as a result,

Which implies a continuity of the function \( f \) at point \( x = a\).

The sign of the derivative indicates the variation

Let \(f\) be a positive continuous function on \(\bigl[a,b \bigr]\), and derivable on \( \hspace{0.1em} ]a,b[\).

Now let \( (x_1, x_2) \in \hspace{0.1em} ]a,b[ \), be two inner points of \( \hspace{0.1em} ]a,b[\) in this order.

In our case,

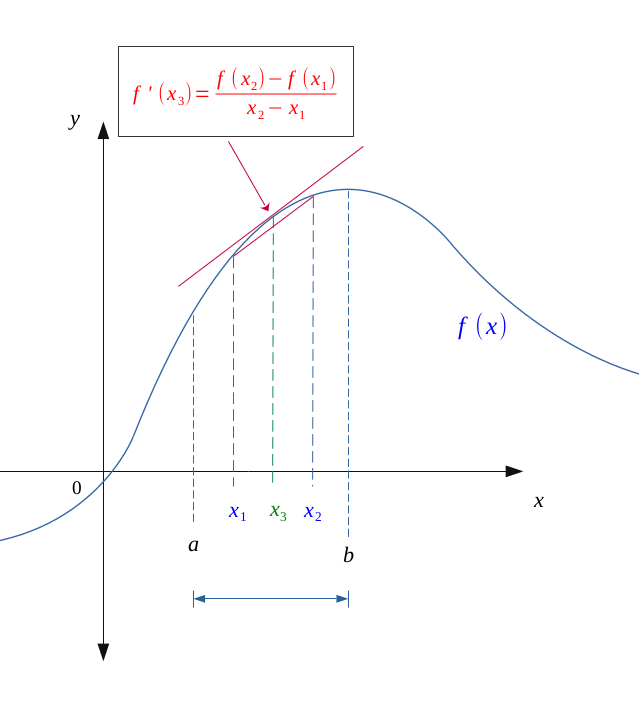
The interval \((x_2-x_1)\) being always positive, if the function \(f\) is increasing on \(\bigl[a,b \bigr]\), it is also the case on \(]x_1, x_2[\), and in this case:

The derivative function \(f'\) will be therefore positive for all \( x \in \bigl[a,b \bigr]\).

The same reasoning can be applied for a decreasing function.

Furthermore, if and only if \(f'\) changes sign between before and after a certain point \(a\), the \(f\) function admits a local extremum at this point.

This formula has to be adapted according to both cases :

Equation of the tangent to the curve at point a

Let's represent a diagram of a function and its tangent, coming from the derived number at the abscissa point \(a\).

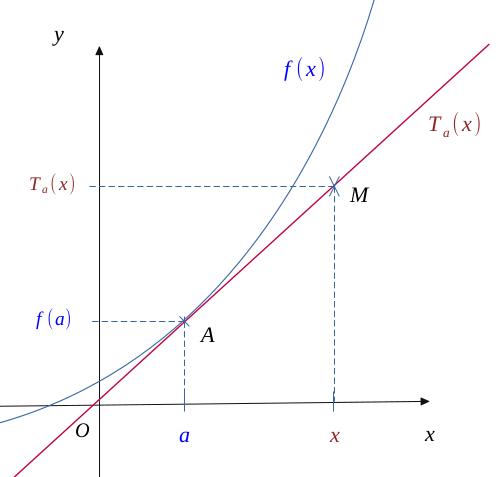
Point \(a\) then has for image \( f(a)\) or \( T_a(a)\)since by definition, a tangent is a point of intersection.

We have also placed a theoretical point \( M(x; T_a(x))\) on the tangent to the curve.

By applying the slope calculation for the points \( A \) and \( B \), we do have:

So, by injecting \( (3) \) into \( (2) \),

And as \( T_a(a) = f(a) \),

The tangent to the curve at the abscissa point \(a\) admits for equation:

Furthermore, in the case of a convexe function, within any interval \(I = [a, b]\), any rope going on either side of these two points is above the curve.

Its tangent can then only be below:

And the inequality will be reversed in the case of a concave function.

Link between Taylor series of order 1 and derivativity

We saw above that the equation to the curve at point \(a\) was worth :

Then, we can represent the curve of this tangent \(T_a\), with that of the study function \(f\), and notice that for any point \(M(x, y)\), there is a difference \(\varepsilon_a(x)\) between these two functions.

1. From left to right implication

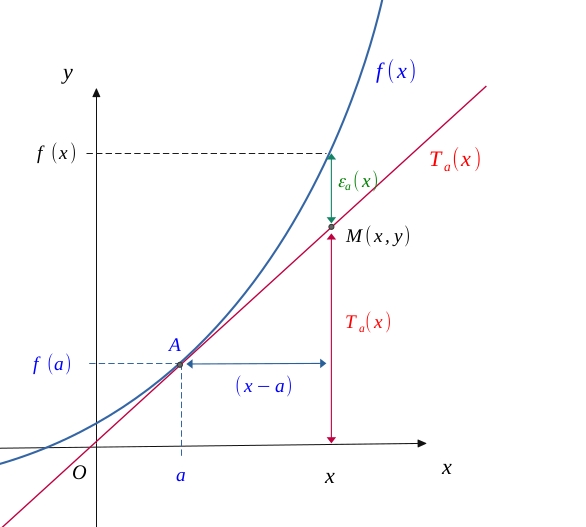
If a function \(f\) admits a Taylor series of order \(1\) at point \(a\) \((TS_n(a))\), then at the neighbourhood of \((x = a)\):

$$ f(x) = f(a) + f'(a)(x-a) + o(x-a) $$
$$ \Bigl( where \enspace o(x-a) = (x-a) \varepsilon(x) \qquad \bigl(with \enspace \lim_{x \to a} \ \varepsilon(x) = 0 \bigr) \Bigr) $$

Which implies the existence of \(f'(a)\). So,

$$ f \ admits \ a \ Taylor \ series \ of \ order \ 1 \ at \ point \ a \ \Longrightarrow \ f \ derivable \ at \ point \ a$$
2. Reciprocal

Now, if a function is derivable at point \(a\), as the previous figure clearly illustrates:

$$ \frac{f(x) - f(a)}{x-a} = \frac{T_a(x) + \varepsilon_a(x) - f(a) }{x-a} $$

Replacing \(T_a(x)\) by its value, we do obtain:

$$ \frac{f(x) - f(a)}{x-a} = \frac{f'(a)(x - a) + f(a) + \varepsilon_a(x) - f(a)}{x-a} $$
$$ f(x) - f(a) = f'(a)(x - a) + \varepsilon_a(x)(x-a) $$

And in the end,

$$ f(x) = f(a) + f'(a)(x - a) + \varepsilon_a(x)(x-a) $$

And since at point \((x=a)\), we do have the equality \(f(x) = T_a (x)\), we do also have that:

$$\lim_{x \to a} \ \varepsilon_a(x) = 0 $$

Which is the definition of a Taylor series or order \(1\). Thus,

$$ f \text{ is derivable at point } a \Longrightarrow f \text{ admits a Taylor series of order 1 at point } a $$
3. Conclusion

The two previous implications give rise to an equivalence, namely:

$$ f \text{ is derivable at point } a \Longleftrightarrow f \text{ admits a Taylor series of order 1 at point } a $$

Example

1. The sign of the derivative indicates the variation

Let us study the variations of a function \(f\) such as:

$$f(x) = \frac{1}{x} - 2\sqrt{x} $$

This function is only defined on: \( D_f = \ ] 0, +\infty[\).

Calculating its derivative \(f'\), we do have:

$$f(x) = \hspace{0.1em} \underbrace{-\frac{1}{x^2}} _\text{ \( < \hspace{0.2em} 0\)} - \hspace{0.1em} \underbrace{\frac{1}{\sqrt{x}} } _\text{ \( < \hspace{0.2em} 0\)} $$

\(f'(x)\) is always negative on \(D_f\).

Thus, \(f(x)\) will be decreasing on this interval.

$$ x $$	$$ 0 $$	$$ \dots $$	$$ +\infty $$
$$ sign \ of \ f' $$	$$ \bigl ]-\infty \bigr] $$	$$- $$	$$ \bigl [ 0^- \bigr] $$
$$ variations \ of \ f $$	$$ \bigl [+\infty\bigr] $$		$$ \bigl ]-\infty \bigr] $$

Furthermore:

$$ \Biggl \{ \begin{gather*} \lim_{x \to 0} \ f(x) = +\infty \\ \lim_{x \to +\infty} \ f(x) = -\infty \end{gather*} $$
$$ \Biggl \{ \begin{gather*} \lim_{x \to 0} \ f'(x) = -\infty \\ \lim_{x \to +\infty} \ f'(x) = \hspace{0.1em} 0^- \end{gather*} $$

Go to the top of the page